1.1.7

Return To Contents
Go To Problems & Solutions

1. An Example

Example 1.1

Find this limit:

Note

Fig. 1.1 As x approaches infinity, (10x + 1)/(2x – 3) appears to approach 5.

The limit appears to be 5. Let's now find it formally.

Solution

EOS

Indeed the limit is 5.

Consider the following four trivial limits:

Go To Problems & Solutions Return To Top Of Page

3. Evaluation Techniques

Dominating Terms

Example 3.1

Determine:

Solution 1

EOS

Solution 2

EOS

In general:

Of course solution 2 is simpler and thus preferable to solution 1.

Example 3.2

Evaluate:

Solution

EOS

Example 3.3

Find:

Solution

EOS

Highest Power Of x In The Denominator

Let's find the same limit as in example 3.1 using a different technique.

Example 3.4

Find:

Solution

EOS

Thus, instead of using the quotient of the dominating terms, we can divide both the numerator and the denominator by
the highest power of x in the denominator. The highest power of x in the denominator in this example is x³.

We note that the dominating-terms technique is simpler and faster than the highest-power-of-x-in-the-denominator
technique. For fractions with long numerator and/or denominator, the dominating-terms technique is preferable.

Return To Top Of Page

Problems & Solutions

1. Find:

Solution



Note

Return To Top Of Page

2. Determine:

Solution



Return To Top Of Page

3. Evaluate:

if it exists.

Solution

Return To Top Of Page

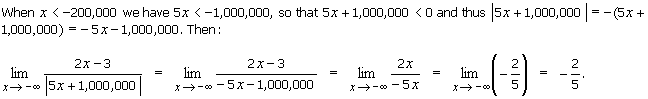
4. Find:

Solution

Return To Top Of Page

5. Determine:

Solution



Return To Top Of Page Return To Contents