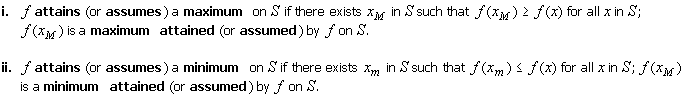Calculus Of One Real Variable – By Pheng Kim Ving
Chapter 1: Limits And Continuity – Section 1.2.2: Extrema

 

1.2.2
Extrema

 

 

Return To Contents
Go To Problems & Solutions

 

1. Maxima and Minima

 

 

Fig. 1.1

 

Maximum of f on [a, b] is f(xM).
Minimum of f on [a, b] is f(xm).

 

Definitions 1.1

 

Let f be a function and S a subset of dom( f ). We say that:

 

 

 

Remarks 1.1

 

i.  A maximum attained by f is a value of f, and so is a minimum attained by f.

 

ii.  S may be any interval, not just a closed finite interval; it may even be a union of a finite number of intervals. The
     definition doesn't require any special type of subset of the domain of f.

 

iii.  f may be continuous at all points of S; it may be discontinuous at some points of S. The definition doesn't require any
     special type of function.

 

Go To Problems & Solutions     Return To Top Of Page

 

2. Attainment Of Extrema

 

An extremum is either a maximum or a minimum. The maximum and minimum are referred to collectively as extrema.
We say that [a, b] is finite if both a and b are finite numbers.

 

Theorem 2.1

 

If a function f is continuous on a closed finite interval [a, b], then it attains both a maximum and a minimum there.

 

 

The proof of this theorem is omitted because it involves more theory than is covered in an introductory calculus course
and therefore is beyond the scope of this tutorial. However, the theorem itself is fairly obvious on an intuitive level.

 

As an example, the function f in Fig. 1.1 is continuous on the closed finite interval [a, b]. It attains both a maximum and
a minimum values there.

 

Remark 2.1

 

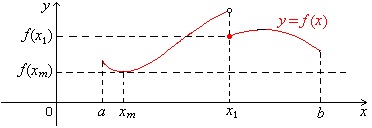
If one or both of the conditions of the theorem are not satisfied, then the conclusion of the theorem need not hold.

 

In Fig. 2.1, f isn't continuous on the closed interval [a, b], but it still manages to attain both a maximum and a minimum
there. However, in Fig. 2.2, f isn't continuous on the closed interval [a, b], and f doesn't attain a maximum there,

 

Fig. 2.1

 

f isn't continuous on [a, b];
f still attains both a maximum f(xM) and a
minimum f(xm) there.

 

Fig. 2.2

 

f isn't continuous on [a, b];
f doesn't attain a maximum there;
f attains a minimum f(xm) there.

 

although it attains a minimum. In Fig. 2.2, the only possible maximum of f would be the value of f at the “ first ” point to
the left of x1, but there's no such point, because if c is a point to the left of x1, then d = (c + x1)/2, which is the middle
between c and x1, is to the left of x1 and closer to x1 than c is.

 

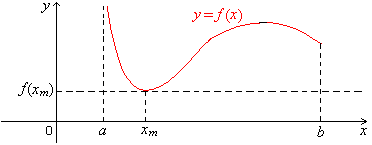
In Fig. 2.3, the interval (a, b] on which f is continuous is half-open, but f still manages to attain both a maximum and a
minimum there. However, in Fig. 2.4, the interval (a, b] on which f is continuous is half-open, and f doesn't attain a
maximum there, although it attains a minimum.

 

Fig. 2.3

 

Interval (a, b] on which f is continuous is
half-open;
f still attains both a maximum f(xM) and a
minimum f(xm) there.

 

Fig. 2.4

 

Interval (a, b] on which f is continuous is
half-open;
f doesn't attain a maximum there, although it
attains a minimum f(xm).

 

 

Example 2.1

 

Find the area of the largest rectangular plot that can be fenced on all sides by 200 m of fence.

 

Note

 

We're asked to find the largest rectangular area that can be enclosed by 200 m of fence, ie, given that the perimeter of a
rectangle is fixed at 200 m, find its dimensions so that its area is the largest.

 

Solution

 

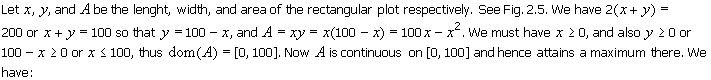
A = 100x – x2 = –(x2 – 100x) = –((x – 50)2 – 2500) = 2500 – (x – 50)2.

 

So A attains the maximum of 2500 when x – 50 = 0 or x = 50. When x = 50 we have y = 100 – 50 = 50. The largest
rectangle is a square of side 50 m and area 2500 m2.

 
Fig. 2.5

 

Rectangular Plot.

EOS

 

Remark 2.2

 

 

Return To Top Of Page

 

Problems & Solutions

 

1.  Let f(x) = x. Does f attain a maximum or a minimum, if so, specify them, on:
     a.  R?
     b.  [1, 2]?
     c.  (1, 2)?
     d.  [1, 2)?
     e.  (1, 2]?

 

Solution

 

a.  No, neither a maximum nor a minimum.
b.  Yes, a minimum of f(1) = 1 and a maximum of f(2) = 2.
c.  No, neither a maximum nor a minimum.
d.  A minimum of f(1) = 1 but no maximum.
e.  A maximum of f(2) = 2 but no minimum.

 

Return To Top Of Page

 

 

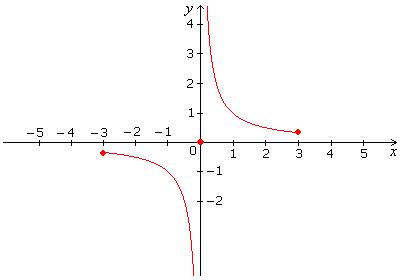
2.  Let:

 

    

 

     a.  What's dom( f )?
     b.  Sketch a graph of f.
     c.  Is f continuous on its domain?
     d.  Does f attain a maximum or a minimum on its domain?

 

Solution

 

a.  dom( f ) = [–1, 1].

 

b.

 

    

 

 

Return To Top Of Page

 

 

3.  Let x and y be any two non-negative numbers with a sum of 8. Show that their product attains both a maximum and
     a minimum. What is the maximum of the product?

 

Solution

 

 

Return To Top Of Page

 

 

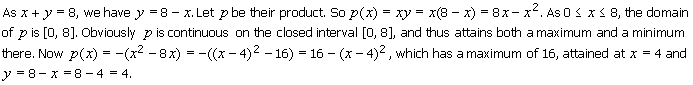
4.  Prove that there's a point on the line:

 

    

 

     that's closest to the origin. Find that point.

 

Solution

 

 

Let P be a point with coordinates (x, y) on the given line, and d the distance from the origin to P. So P is closest to the
origin when d attains its minimum value. We have:

 

 

Return To Top Of Page

 

 

5.  Let f(x) = anxn + an–1xn–1 + an–2xn–2 + ... + a1x + a0, where n is an even positive integer and an > 0. Prove that f
     attains a minimum over the entire real line.

 

Solution

 

We have:

 

 

Return To Top Of Page     Return To Contents