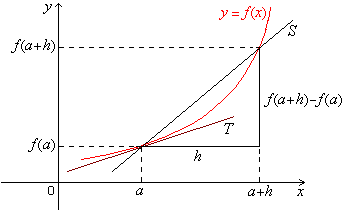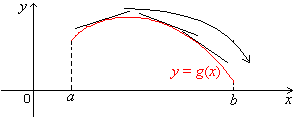|
Calculus Of One Real Variable By Pheng Kim Ving |
|
2.3 |
Return To Contents
Go To Problems & Solutions
|
1. Rates Of
Change And Slopes |
|
|
In Section
2.1, we see that the |
slope of secant S and the slope of tangent T to the graph of f at x = a are:
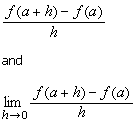
respectively. In Section
2.2, we see that the average rate of change of f over [a, a + h] and the instantaneous rate of change of f at x = a are:
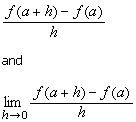
respectively, which are the same as the 2
quantities above.
So the geometric interpretation of the
average rate of change of f over [a, a + h] is the slope of the
secant thru points
(a, f(a)) and (a + h, f(a + h)), and the geometric interpretation of the
instantaneous rate of change of f at x = a
is
the
slope of the tangent to the graph of f at x = a.
|
|
Instantaneous rate of change
and slope of tangent Derivative is instantaneous
rate of change and slope |
Using Two-Sided limits
Since the instantaneous rate of
change is unique if it exists, the limit involved in its definition is a
two-sided limit, not
one-sided limits, which may be different when both exist. Similarly, since the
tangent line is unique if it exists, the limit
involved in the definition of its slope is a two-sided limit. So the h in their definitions must take on both
positive and
negative values. In the above discussion, we implicitly assume h > 0, so that a < a + h, the interval is [a, a + h], and the
limit is that of the difference quotient:
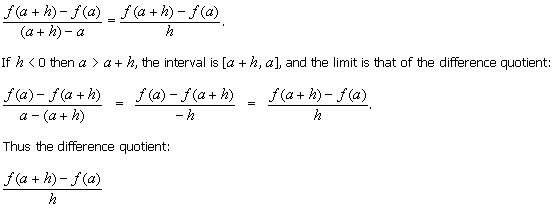
is valid for both positive and
negative values of h.
Go To Problems &
Solutions Return
To Top Of Page
|
2. The
Derivative |
The slope of the tangent line to a straight line
is the same at every point. The slope of the tangent line to the portion of
the graph of y = f(x) displayed in Fig. 1.1 changes from point to point. We've got a
quantity, the slope of the tangent line,
that may change, ie, we've got a function. Thus, it's useful to give it a
technical name. That name is derivative, which
derives from the verb derive .
Definitions 2.1
|
This limit is called the derivative of f or the derivative of f with respect to
x at a. (If it exists, then the derivative
exists; if it doesn't exist, then the derivative doesn't exist.) See Fig. 1.1. The derivative f '(x) of f at any point x in the
The quantity f '(x) may depend on x, so that f '(x) is a function
of x. The function f '(x) is called the derivative of f If f '(a) exists, then f is said to be differentiable
at a. If f is differentiable at every point in its domain,
then it's To find the derivative f ' of a function f is called to differentiate
f. The process of differentiating a function is called |
Remarks 2.1
ii. The
derivative f '(a) is the instantaneous rate of change of f at x = a and the slope of the tangent line to the
graph of f
at x = a.
iii. The
derivative f '(a) is the value of the derivative (function) f '(x) at x = a.
iv. The
derivative of a function f is a function
that derives from f, hence the name derivative.
![]()

|
3. Derivatives Of Some Elementary Functions |
We now prove that the
derivatives of the functions in the first column are as shown in the second
column in the following
table, where sgn, read sig-nem, is the signum (Latin for
sign) function and is defined by:
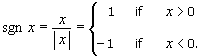
|
|
Proof
For
f(x) = C:
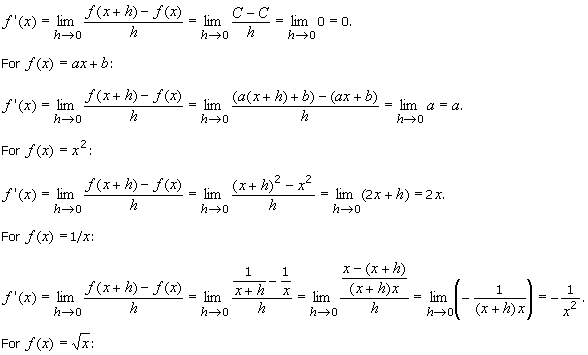
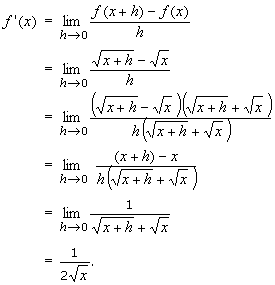
For f(x) = |x|. If x > 0 then f(x) = x so that f '(x) = 1 ( f(x) = ax + b, a = 1 and b = 0). If x < 0 then f(x) = x so
that f '(x) = 1. Hence f '(x) = sgn x.
EOP
Note that from Section
2.1.2 Where There Are No Tangent Lines it follows that the function f(x) = |x| isn't
differentiable at x = 0. So we leave sgn x undefined at x = 0.
Go To Problems &
Solutions Return
To Top Of Page
|
4. Notations
For Derivatives |
The derivative of the function y = f(x) is denoted in several ways as follows:
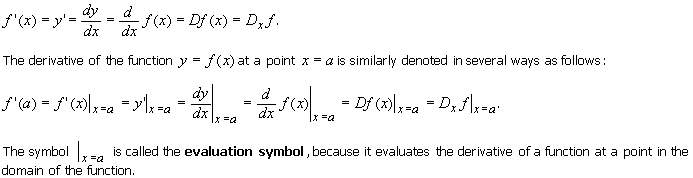
The Leibniz
Notation
The notation:
![]()
is called the Leibniz notation. It's
read derivative of y with respect to x , or, for short, dee y over dee x . It's
suggestive of the fact that the derivative of y with respect to x is the rate of
change of y with respect to x. For now,
regard it as a single symbol, not as a
quotient. The quotient interpretation will appear in later sections and
chapters.
Go To Problems &
Solutions Return
To Top Of Page
|
5. Equations
Of Tangent Lines |
Recall that the equation of a straight line
passing thru the point (x0, y0) and having slope m is y = m(x x0) + y0; see
Section
2.1.2. Hence the equation of the tangent line to the graph of f at x = x0 is:
y = f '(x0)(x x0) + f(x0).
The equation of the tangent line T in Fig. 1.1 is y = f '(a)(x a) + f(a).
Example 5.1
Find the equation of the tangent
line to the curve y = x2 at x = 3.
Solution
The
slope of the tangent line is y'|x=3 = 2x|x=3 =
2(3) = 6. When x = 3
we have y = 32 = 9.
The equation of the tangent
line is y = 6(x 3)
+ 9, or y = 6x 9.
EOS
Go To Problems &
Solutions Return
To Top Of Page
|
6. Obtaining
Graphs Of Derivatives From Those Of Functions |
Let f be differentiable
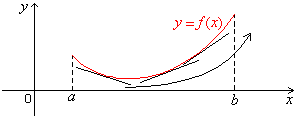
on (a, b). See Fig. 6.1. The graph of f
opens upward. We note that as x increases from a to b,
the
tangent line to the graph of f at x turns counterclockwise,
which means that its slope and thus the derivative f '(x)
|
|
Fig.
6.1
The graph of f opens upwayd on (a, b).
|
|
|
Fig.
6.2
The graph of g opens downward on (a, b).
|
increase. Let g be differentiable
on (a, b). See Fig. 6.2. The graph of g
opens downward. We note that as x increases
from a to b, the tangent line to the graph of g
at x turns clockwise, which means that its slope and thus the
derivative
g'(x)
decrease.
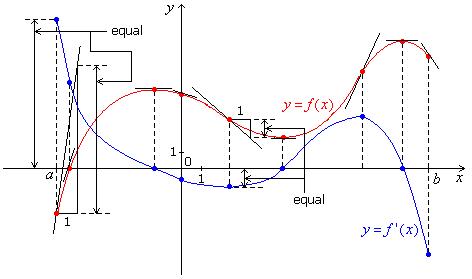
Suppose we wish to sketch a
graph of the derivative f ' of a
function f on an interval [a, b] by
using the graph of f on [a,
b]. See Fig. 6.3. For this task,
we find an enough number of points (x, f '(x)) and join them by a curve that will
be the
|
|
Fig. 6.3 Graph Of y = f(x). |
|
|
Fig. 6.4 Obtaining Graph Of y = f '(x)
From |
graph of f '.
Since at any point x of [a, b] the
value f '(x) is the slope of the tangent line to
the graph of f at x, we select
a number of points (x, f(x)) on
the graph of f and at
each of them estimate the slope f '(x) of the tangent line to the
graph of f at that point, then we plot the
point (x, f '(x)). Refer to Fig. 6.4. The selected
points include:
the endpoints of the interval,
the x-intercepts
and y-intercept of the graph of f,
the points (x, f(x)) where the tangent line to the graph
of f is horizontal and thus has
slope f '(x) = 0 so that the point
(x, 0)
is the x-intercept of the graph of f ', and
points in each sub-interval formed by
these x-intercepts of the graph of f ' where
the graph of f
changes from opening
upward to opening downward or
respectively from opening downward to opening upward so that f '(x) changes from
increasing to decreasing or
respectively from decreasing to increasing there and hence the graph of f ' has a
maximum
or respectively a minimum there; at
each of such points the tangent line to the graph of f crosses the graph of f.
Of course more points on the
graph of f have to be selected if it's
necessary to do so for the shape of the graph of f ' to
be revealed.
To estimate the slope of the
tangent line to the graph of f at a
point x, we draw a short tangent line
to the graph of f at
the point (x, f(x)), draw a short horizontal line
segment from the point (x, f(x)) to
the right with length 1, and draw a
vertical line segment from the right endpoint of that horizontal line segment
to the tangent line, then, as slope = rise/run
= rise/1 = rise, we estimate the signed length of that vertical line segment,
which is positive if the vertical line segment is
upward toward the tangent line or negative if it's downward, and that's the
desired slope.
After getting enough points (x, f '(x)), we join them together by a curve,
which is the graph of f '.
Let y = f(x).
Suppose x is increasing on a
sub-interval, so that the change in x is
positive on that sub-interval. If y is
also
increasing, then the change in y is
also positive, therefore (change in y)/(change
in x) > 0, and it must be that f '(x) =
dy/dx > 0
at any point x of
the sub-interval, thinking of dx as a
small change in x and dy as the corresponding small
change in y. If y is
instead decreasing, then the change in y is
negative, therefore (change in y)/(change
in x) < 0, and it
must be that f '(x) = dy/dx < 0 at any point x of the sub-interval. If y is constant, then the change in y is 0, therefore
(change in y)/(change in x) = 0, and it must be that f '(x) = dy/dx = 0 at any point x of the sub-interval. Thus make
sure that the following verification is satisfied:
on any sub-interval where f is
increasing, the graph of f ' is
above the x-axis,
on any sub-interval where f is decreasing, the graph of f ' is
below the x-axis, and
on any sub-interval where f is constant, the graph of f ' is a
line segment on the x-axis.
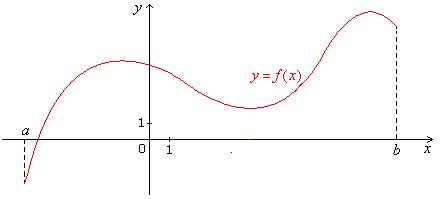
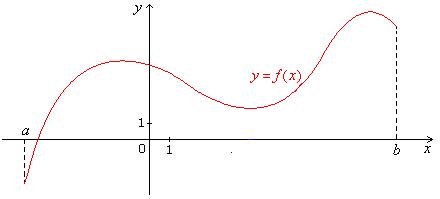
Example 6.1
A graph of y = f(x) is given in Fig. 6.5. Use it to
sketch a graph of the derivative y = f '(x).
|
|
Fig. 6.5 Graph Of y = f(x). |
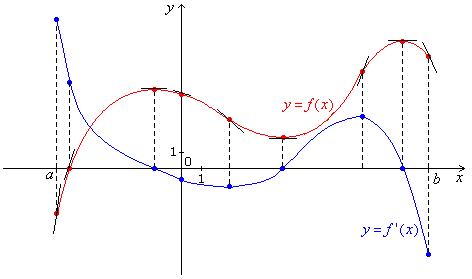
Solution
The
graph of y = f '(x) as obtained from that of y = f(x) is sketched in Fig. 6.6.
|
|
Fig. 6.6 Graph Of y = f '(x)
Obtained From |
EOS
|
Problems
& Solutions |
1.
i. Using a calculator, find the
slope of the secant line to f(x) = x3 2x passing thru the points corresponding to x = 2
and x = 2 + h, where:
a. h =
0.1.
b.
h = 0.01.
c. h = 0.001.
ii. Guess f '(2).
iii. Calculate f '(2) directly from the
definition of derivative.
Solution
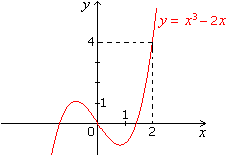
Note that f(2) =
23 2(2) = 4.
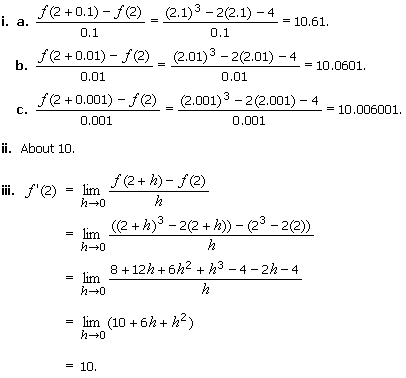
![]()
2.
Differentiate each of the following functions directly from the
definition of the derivative.
a. f(x) = 1 +
4x 5x2.
b. g(t) = (t2 3)/(t2 + 3).
c. h(x) = x + |x 1|.
Solution
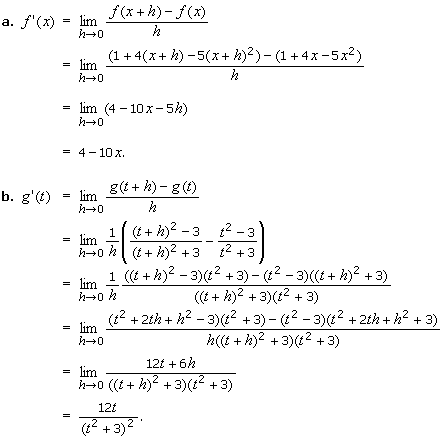
c. The graph of y = h(x) = x + |x 1| has a sharp point
at x = 1. We'll show
that h has a derivative
everywhere on R
except at x = 1.
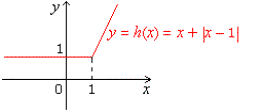
If x 1
> 0
or x > 1, then | x 1| = x 1, so h(x) = x + (x 1) = 2x 1, thus:
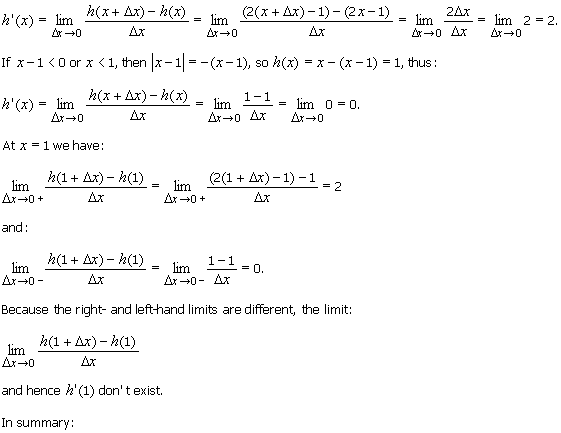
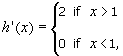
h'(1)
doesn't exist.
Notes
![]()
3.
Calculate:
![]()
directly
from the definition of the derivative.
Solution
Let f(x) = x1/3. Then:
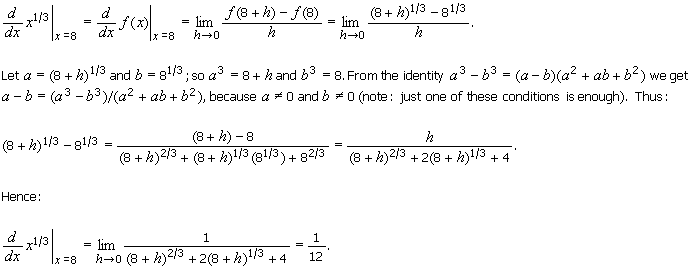
![]()
4.
Utilizing the definition of derivative, find an equation of the tangent
line to the curve y
= 2/(t2
+ t) at the point where
t
= 1.
Solution
At t = 1 we have y = 1. The slope of the
tangent line at t = 1 is:
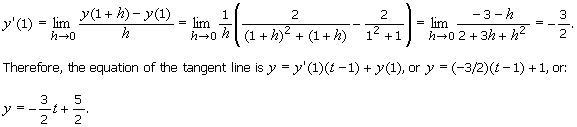
Note
The notation y(E ), where E is an expression, means the value of y at t = E, not the product yE. This notation is similar
to the notation f(t). It treats y as a function of t. Similarly for
the notation y'(E ).
![]()
5. The graph of f is
given in the figure below. Use it to sketch a graph of the derivative f '.
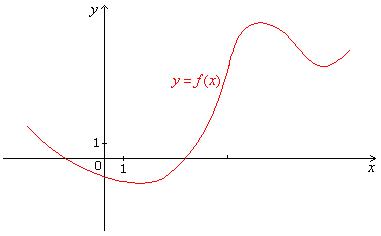
Solution
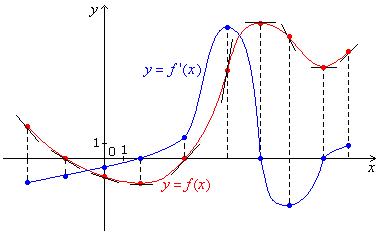
![]()
6.
Prove that:
a. The
derivative of an even differentiable function is odd.
b. The
derivative of an odd differentiable function is even.
Solution
a. Let
f be an even
differentiable function and x an arbitrary point in its domain. Then:
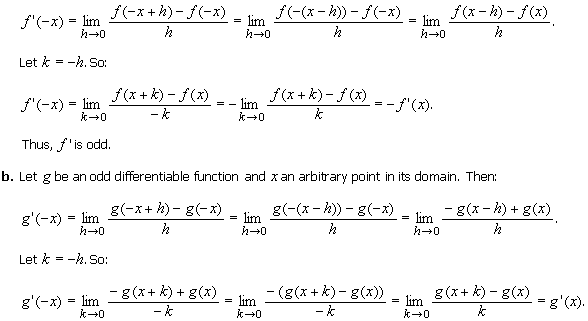
Thus, g' is even.
Return To Top Of Page Return To Contents