Calculus Of One Real Variable – By Pheng Kim Ving
Chapter 2: The Derivative – Section 2.4: Differentiability Vs Continuity

 

2.4
Differentiability Vs Continuity

 

 

Return To Contents
Go To Problems & Solutions

 

1. Differentiability Implies Continuity

 

We'll show that if a function is differentiable, then it's continuous.

 

Theorem 1.1

 

If a function f is differentiable at a point x = a, then f is continuous at x = a.

 

 

Proof

EOP

 

Note that if we let h = x – a then:

 

 

The right-hand side of the above equation looks more familiar: it's used in the definition of the derivative.

 

Go To Problems & Solutions     Return To Top Of Page

 

2. Continuity Doesn't Imply Differentiability

 

We'll show by an example that if f is continuous at x = a, then f may or may not be differentiable at x = a. The converse
to the above theorem isn't true. Continuity doesn't imply differentiability.

 

Example 2.1

 

 

Solution
a.

Fig. 2.1

 

 

 

 

     and thus f '(0) don't exist. It follows that f is not differentiable at x = 0.

 

Remark 2.1

 

In handling continuity and differentiability of f, we treat the point x = 0 separately from all other points because f changes
its formula at that point. We do so because continuity and differentiability involve limits, and when f changes its formula at
a point, we must investigate the one-sided limits at both sides of the point to draw the conclusion about the limit at that
point.

 

Go To Problems & Solutions     Return To Top Of Page

 

3. Where Functions Aren't Differentiable

 

 

Fig. 3.1

 

f isn't differentiable at a where it's discontinuous, at b where its
graph has a sharp point, and at c where its graph has a vertical
tangent line.

 

Return To Top Of Page

 

Problems & Solutions

 

1. Let y = f(x) = x1/3.
    a.  Sketch a graph of f using graphing technology.
    b.  Based on the graph, where is f both continuous and differentiable?
    c.  Based on the graph, where is f continuous but not differentiable?

 

Solution

a.

 

 

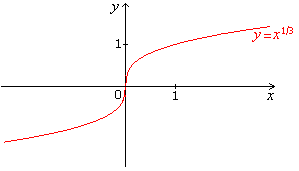
b.  Based on the graph, f is both continuous and differentiable everywhere except at x = 0.

 

c.  Based on the graph, f is continuous but not differentiable at x = 0.

 

Return To Top Of Page

 

 

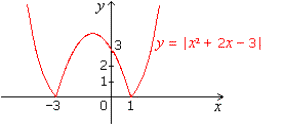
2.  Let f be defined by f(x) = |x2 + 2x – 3|.
     a.  Show that f is continuous everywhere.
     b.  Show, using the definition of derivative, that f is differentiable everywhere except at x = – 3 and x = 1.

 

Solution

 

a.  We have f(x) = |(x + 3)(x – 1)|. The following table shows the signs of (x + 3)(x – 1).

 

   

 

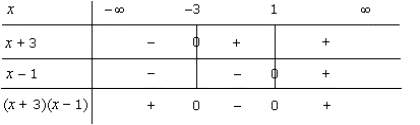
    So we have:

 

    

 

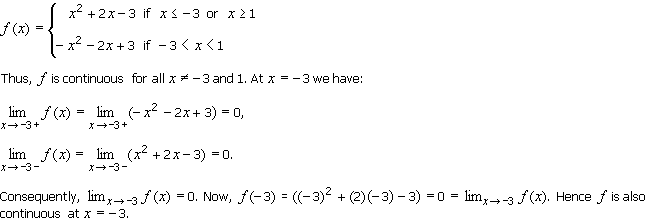
    Similarly, f is also continuous at x = 1. It follows that f is continuous everywhere.

 

b.

 

     Case Where x < – 3 Or x > 1.  We have:

 

    

 

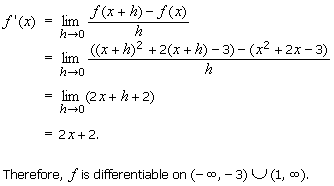
     Case Where – 3 < x < 1.  We have:

 

    

 

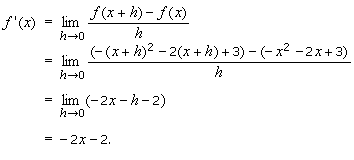
     So f is differentiable on (– 3, 1).

 

     Case Where x = – 3.  We have:

 

    

 

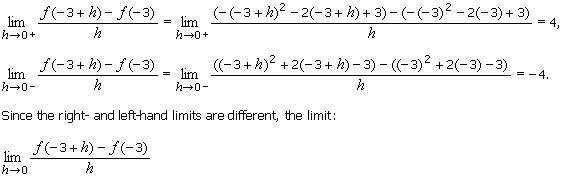
     and thus f '(– 3) don't exist. As a consequence, f isn't differentiable at x = – 3.

 

     Case Where x = 1.  Similarly, f isn't differentiable at x = 1.

 

     In summary, f is differentiable everywhere except at x = – 3 and x = 1.

 

Return To Top Of Page

 

 

 

Solution

 

 

 

Note

 

Many other examples are possible, as seen in the figure below.

 

 

Return To Top Of Page

 

 

 

Solution

 

 

 

Return To Top Of Page

 

 

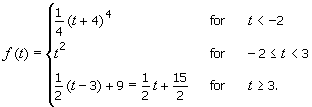
5.  If possible, give an example of a differentiable function that isn't continuous.

 

Solution

 

That's impossible, because if a function is differentiable, then it must be continuous.

 

Return To Top Of Page     Return To Contents