Return
To Contents
Go To Problems & Solutions
|
1. Derivatives Of Sine And Cosine |
Let's find the derivatives of the
sine and cosine functions sin x and cos
x, where the angle x
is in radians. Since at this
level sin x and cos
x aren't expressed in terms of functions whose
derivatives we already know, we have to go back to
the definition of the derivative as a limit. We have:
|
|
|
|
|
|
|
|
Necessity Of The Radian Measure
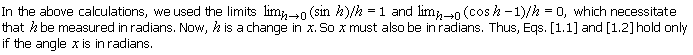
Go To Problems & Solutions Return To Top Of Page
|
2. Derivatives Of Tangent, Cotangent, Secant, And Cosecant |
We derive the derivatives of the 4
remaining trigonometric functions, namely the tangent, cotangent, secant, and
cosecant functions, from those of the sine and cosine functions. That of the
cotangent function is derived indirectly.


|
|
The derivations of these equations are based on Eqs. [1.1] and [1.2]. Consequently they also hold only if x is in radians.
Go To Problems & Solutions Return To Top Of Page
|
3. Memorizing The Derivatives |
It's recommended that you memorize
the derivatives of the six trigonometric functions, in the same fashion that
you do
those of ax or xn.
Let's gather all six of them here.
(sin
x)' = cos x, (tan x)'
= sec2 x,
(sec x)' = sec
x tan x,
(cos x)' = – sin
x, (cot
x)'
= – csc2 x,
(csc x)' = – csc
x cot x.
We say that cos
x is the cofunction of sin x, and that sin
x is the cofunction of cos x; thus sin
x and cos x are
cofunctions of each other. Similarly, tan
x and cot x
are cofunctions of each other, and sec x
and csc x are
cofunctions
of each other.
We note that:
a. The derivatives of sin x, tan x, and sec x don't have a minus sign, while those of their respective cofunctions do.
b. The derivatives of sin x, tan x,
and sec x are cos
x, sec2 x, and sec x
tan x
respectively. The derivative of the
cofunction of any of them is obtained by adding a minus sign and changing each
function in the derivative to its
cofunction.
Go To Problems & Solutions Return To Top Of Page
|
4. When The Angle Isn't In Radians |
We repeat it here that the
formulas for the derivatives of the trigonometric functions given so far
require that the angle be
in radians. We're now going to see two particular derivatives when the angle is
in degrees.
Example 4.1
Differentiate sin
xo and cos xo. Note that the
angle is measured in degrees. Use the degree measure for the angle in your
answers.
Solution
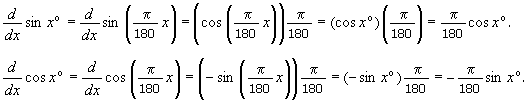
EOS
|
Problems & Solutions |
1. Differentiate each of the following functions.
a. y = cot (4 – 3x).
b. f(x)
=
sin3
cos (x/3).
Solution

![]()
2.
Differentiate each of the following functions. Note that the angles are
measured in degrees. Use the degree measure
for the angles in your answers.
![]()
Solution
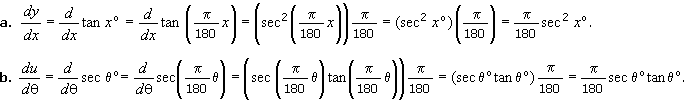
![]()
3. Find an equation of the tangent line to each of the following curves at the indicated point.
![]()
Solution
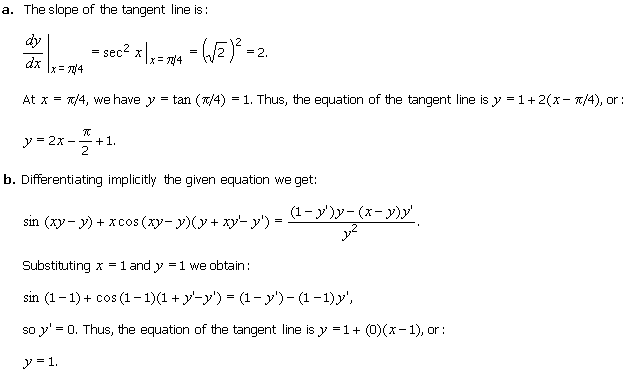
![]()
4. Let z = tan (x/2). Prove that:
![]()
Solution
Let's treat the equation:
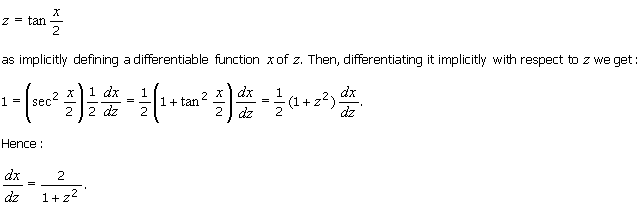
![]()
5. Let y = sin ax, where a is a constant.
a. Calculate
the first eight derivatives of y.
b. Guess a formula for the nth derivative of y, for any n in N.
c. Prove your guess using mathematical induction.
Solution
a. y' = (cos
ax)a = a cos ax,
y''
= a(– sin ax)a = – a2 sin ax,
y''' = – a2(cos ax)a = – a3 cos ax,
y (4) = – a3(– sin ax)a = a4 sin ax,
y (5) = a4(cos ax)a = a5 cos ax,
y (6) = a5(– sin ax)a = – a6 sin ax,
y (7) = – a6(cos ax)a = – a7 cos ax,
y (8) = – a7(– sin ax)a = a8 sin ax.
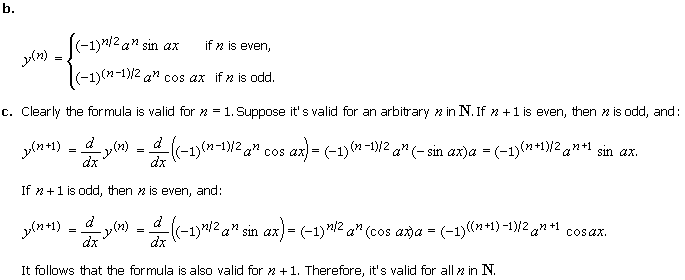
Return To Top Of Page Return To Contents



