Calculus Of One Real Variable
By Pheng Kim Ving
Chapter 7: The Exponential And Logarithmic Functions
Section 7.3: General Exponential And Logarithmic Functions

7.3
General Exponential And Logarithmic Functions

Return To Contents
Go To Problems & Solutions

1. The General Exponential Functions

Since the natural exponential function e^x is differentiable, it's continuous. Its range is all y > 0. So if b is a positive number, the
Intermediate-Value Theorem assures that there exists k such that e^k = b. Thus b^x = (e^k)^x = e^kx. Now because e^k = b, we have
k = ln b. Consequently, b^x = e^{(ln b)x} = e^{x ln b.}. Note that the equation b^x = e^{x ln b.} can also be obtained as follows: as e^x and ln x are
inverses of each other, we have b = e^{ln b}, hence b^x = (e^{ln b.})^x = e^{x ln b}. We define b^x to be e^{x ln b.}.

Definition 1.1 - General Exponential Functions

For any b > 0 and for any x we define b^x by:

The function y = b^x is called the exponential function of base b. The general exponential function refers to the exponential function y = b^x where the base b can be any positive number. Recall that the natural exponential function y = e^x is the exponential function of the particular base e.

Recall that the reason why we require that b > 0 is that we want b^x to be defined for all x. If b = 0, b^x isn't defined for x = 0
(form 0⁰ isn't defined) or for any x < 0 (no fraction can have denominator 0). If b < 0, b^x isn't defined as a real number at for
example x = 1/2 (no negative number has a real square root). So b^x is defined for all x only if b > 0. Another way to see this
requirement is Eq. [1.1], where we use ln b, requiring that b > 0.

Go To Problems & Solutions Return To Top Of Page

2. Properties Of The General Exponential Functions

The following properties of b^x are similar to those of e^x as discussed in Section 7.1 Theorem 6.1.

Theorem 2.1 – The Laws Of Exponents

For any b > 0 and for any x and y we have:

Proof
Let's do the proof for part a. Those for the remaining formulas are similar to it. We have:

b^xb^y = e^{x ln b}e^{y ln b} = e^{x ln b + y ln b} = e^{(x+y) ln b} = b^x+y.
EOP

the Natural Logarithm Of The General Exponential

In Section 7.2 Theorem 2.1 Part d, we had ln x^t = t ln x for any x > 0 and for any t. That's the natural logarithm of a power
function. The formula is also true for the natural logarithm of an exponential function.

Theorem 2.2 - Natural Logarithm Of General Exponential

For any b > 0 and for any x we have:

ln b^x = x ln b.

Proof
ln b^x = ln e^{x ln b} = x ln b.
EOP

Example 2.1

Solve 3^x = 9^1–x.

Solution
3^x = 9^1–x,

ln 3^x = ln 9^1–x,

x ln 3 = (1 – x) ln 9,

x( ln 3 + ln 9) = ln 9,

EOS

Solving an equation containing exponential expressions like in this example can be performed by taking of the natural
logarithm of both sides of the equation.

Go To Problems & Solutions Return To Top Of Page

3. Differentiation Of The General Exponential Functions

We know that (d/dx) e^x = e^x. In Section 7.1 Introducing e, we got (d/dx) b^x = kb^x, where e^k = b. Since e^k = b, we have k =
ln b. So (d/dx) b^x = (ln b) b^x = b^x ln b.

Theorem 3.1 – The Exponent Rule

For any b > 0 and for any x we have:

This differentiation formula is called the exponent rule.

Proof
Using the chain rule on e^{x ln b} we get:

EOP

Remark 3.1

Again note that (d/dx) b^x is not xb^x–1!! Keep in mind that b^x is an exponential function, not a power function.

Example 3.1

If y = 2^{3x + 1}, find y'.

Solution

y' = 2^{3x + 1}( ln 2)(3) = 3( ln 2)2^{3x + 1}.

EOS

Go To Problems & Solutions Return To Top Of Page

4. The General Power Rule

Now let's take a look back at the power functions and extend the power rule. We saw in Section 3.2 Corollary 4.1 that
(d/dx) xⁿ = nx^n–1 for all integer n. We saw in Section 3.3 Corollary 4.1 that (d/dx) (u(x))^r = r(u(x))^r–1(du/dx) for any
rational number r, from which we have (d/dx) x^r = rx^r–1 for any rational number r. We now show that (d/dx) x^a = ax^a–1
for any real number a, rational or irrational.

Theorem 4.1 – The General Power Rule

For any constant a we have:

This differentiation formula is called the general power rule.

Proof

EOP

Remarks 4.1

Go To Problems & Solutions Return To Top Of Page

5. Graphs Of General Exponential Functions

Example 5.1

Sketch a graph of y = 2^x, using information obtained from the equation.

Solution

Some More Points: (-2, 1/4), (-1, 1/2), (1, 2), (2, 4).

The graph is sketched in Fig. 5.1.

Fig. 5.1 Graph Of y = 2^x.

EOS

Example 5.2

Sketch a graph of y = (1/2)^x, using information obtained from the equation.

Solution

Some More Points: (-2, 4), (-1, 2), (1, 1/2), (2, 1/4).

The graph is sketched in Fig. 5.2.

Fig. 5.2 Graph Of y = (1/2)^x.

EOS

General Case

y = b^x, b > 0.

Case 0 < b < 1. (Think of the graph of y = (1/2)^x in Fig. 5.2 where b = 1/2)

Inflection Points: None.

Case b > 1. (Think of the graph of y = 2^x in Fig. 5.1 where b = 2)

Inflection Points: None.

The graphs of y = 2^x, y = (1/2)^x, y = 10^x, y = (1/10)^x, y = e^x, and y = 1^x = 1 are sketched in Fig. 5.3. Remark that the graphs
of all exponential functions of the form y = b^x go thru the y-intercept (0, 1) as b⁰ = 1 for all b > 0.

Fig. 5.3 Graphs Of Some Exponential Functions. Graphs of all exponential functions y = b^x go thru the y-intercept (0, 1).

Go To Problems & Solutions Return To Top Of Page

6. The General Logarithmic Functions

The natural logarithm function is defined as the inverse of the natural exponential function. So it's perfectly natural to define
the general logarithmic function as the inverse of the general exponential function.

Consider y = 2^x, the exponential function of base 2, as graphed in Fig. 5.1. Clearly it's one-to-one, and so has an inverse. This
inverse is called the logarithmic function of base 2 or logarithm of base 2, and denoted log ₂. Thus if y = 2^x then x = log ₂ y.
Consequently log ₂ y = exponent on 2 (exponent to which 2 is raised) to get y. The function 1^x isn't one-to-one and hence has
no inverse. Hence there's no logarithm with base 1 (1^x is always 1, can't be 2 or 10 or any number other than 1). In relation
[6.1] below, we exchange the roles of the letters x and y to conform to the standard presentation of the definition of an
inverse function.

Definition 6.1 - General Logarithmic Functions

So log_b x = exponent on b to get x.

The general logarithmic function refers to the logarithmic function y = log_b x, where the base b can be any real number that's positive and different from 1.

Properties

Properties

Remarks 6.1

a. In “... the exponent on b to get x”, the quantity appearing after “to get”, x in this case, isn't the function (output), it's the
variable (input).

b. The logarithmic function might just as well be called the “ exponent function”. It isn't, because calling it so would create
confusion with the exponential function.

The Natural Logarithm Is The Logarithm Of Base e

By Definition 6.1, the inverse of the natural exponential function e^x of base e is the logarithm function log_e of base e. We know
that this inverse is the natural logarithm function ln. So the natural logarithm function is the logarithm function of the particular
base e.

Natural Logarithm Is Logarithm Of Base e

The natural logarithm function is the logarithm function of base e:

ln x = log_e x.

Go To Problems & Solutions Return To Top Of Page

7. Properties Of The General Logarithmic Functions

The following properties of the general logarithmic functions except the last one are similar to the corresponding properties of
the natural logarithm function as discussed in Section 7.2 Theorem 2.1. One of the properties of the general logarithmic
functions that we're going to state and prove is log_b xy = log_b x + log_b y. This relation expresses the logarithm of the product
xy of 2 numbers x and y in terms of the logarithms of the original numbers x and y. This property says that the logarithm of
the product of 2 numbers equals the sum of the logarithms of the original numbers.

Theorem 7.1 - Properties Of General Logarithmic Functions

Proof

a. Let y = log_b 1. Then b^y = 1 = b⁰. So log_b 1 = y = 0. (Intuitively, the exponent on b to get 1 is 0.)

b. Let y = log_b b. Then b^y = b = b¹. So log_b b = y = 1. (Intuitively, the exponent on b to get b is 1.)

c. Let p = log_b x and q = log_b y, so that x = b^p and y = b^q. Then log_b xy = log_b b^pb^q = log_b b^p+q = p + q = log_b x + log_b y.

d. log_b x + log_b (1/x) = log_b (x(1/x)) (by part c) = log_b 1 = 0. So log_b (1/x) = - log_b x.

e. log_b (x/y) = log_b (x(1/y)) = log_b x + log_b (1/y) (by part c) = log_b x - log_b y (by part d).

f. Note that if t is a positive integer then, by repetitive applications of part c:

For t = 0, we have log_b x⁰ = log_b 1 = 0 = 0 log_b x.

For any non-0 real number t. Let y = log_b x^t, so that x^t = b^y. Then x = b^y/t, then y/t = log_b x, then y = t log_b x. Thus
log_b x^t = t log_b x.

Consequently, for any real number t we have log_b x^t = t log_b x.

g. Let y = log_b x. Then x = b^y. So log_c x = log_c b^y = y log_c b (2nd equation is by part f). Thus log_b x = y = (log_c x)/( log_c b).

EOP

Corollary 7.1 - Logarithms Of Extended Products And Quotients

For any real p_i, any real q_j, any positive integer m, and any positive integer n we have:

Proof

EOP

Example 7.1

Solution

EOS

Go To Problems & Solutions Return To Top Of Page

8. Differentiation Of The General Logarithmic Functions

Theorem 8.1

Proof

EOP

Derivatives Of Exponentials And Logarithms

For help in the distinction and memorization of the derivatives of the exponential and logarithmic functions, we gather them
together in the following table.

Derivatives Of Exponentials And Logarithms

Example 8.1

Differentiate:

Solution 1

EOS

Solution 2

EOS

In Solution 2 we first simplify the function expression before differentiating. This simplifies the differentiation greatly.
Solution 2 is simpler than Solution 1 and for this reason is preferable.

Go To Problems & Solutions Return To Top Of Page

9. Graphs Of The General Logarithmic Functions

Graphs Of Inverses

Fig. 9.1 b > 1, graph of y = logb x is reflection of that of its inverse y = b^x about line y = x.

Fig. 9.2 0 < b < 1, graph of y = logb x is reflection of that of its inverse y = b^x about line y = x.

Graph Of y = ln x

Fig. 9.3 Graph Of y = ln x.

Example 9.1

Sketch a graph of y = log₂ x, using information from the equation.

Solution

Inflection Points. Since there's no change of concavity, there's no inflection point.
Some More Points: (1/4, -2), (1/2, -1), (4, 2), (8, 3). ( y = exponent on 2 to get x, so choose x-values that are integer powers
of 2 such that it's easy to determine y mentally.)

The graph of y = log₂ x is sketched in Fig. 9.4.

Fig. 9.4 Graph Of y = log2 x.

EOS

Example 9.2

Sketch a graph of y = log_1/2 x, using information from the equation.

Solution

Inflection Points. Since there's no change of concavity, there's no inflection point.
Some More Points: (1/4, 2), (1/2, 1), (2, -1), (4, -2), (8, -3).

The graph of y = log_1/2 x is sketched in Fig. 9.5.

Fig. 9.5 Graph Of y = log1/2 x.

EOS

General Case

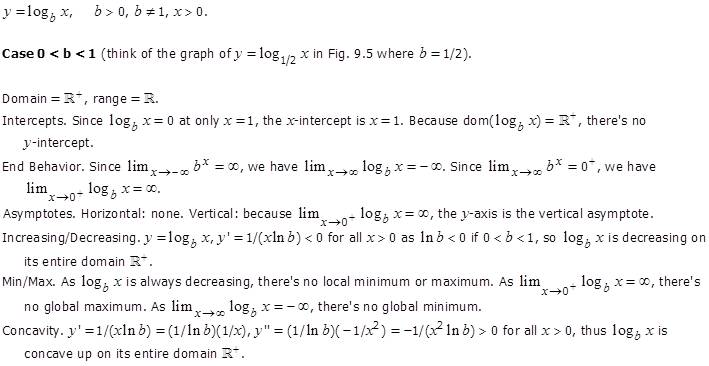
Inflection Points. Since there's no change of concavity, there's no inflection point.

Case b > 1. (Think of the graph of y = ln x in Fig. 9.3 where b = e > 1 or the graph of y = log₂ x in Fig. 9.4 where b = 2)

Inflection Points. Since there's no change of concavity, there's no inflection point.

Graphs

The graphs of some logarithmic functions are sketched in Fig. 9.6. Remark that the graphs of all the basic logarithmic
functions go thru the x-intercept (1, 0) ( y = log₂ x is a basic logarithmic function, while y = 3 log₂ x - 4 isn't; it's a
transformed logarithmic function). A way to help memorize the shape of the graph is the graphs of y = ln x = log_e x and
y = log_1/2 x: since e > 1, the graph of y = log_b x where b > 1 has a similar shape as that of y = ln x; since 0 < 1/2 < 1,
the graph of y = log_b x where 0 < b < 1 has a similar shape as that of y = log_1/2 x. So memorize the graphs of y = ln x
and y = log_1/2 x.

Fig. 9.6 Graphs Of Some Logarithmic Functions. Graphs of all logarithmic functions y = logb x go thru x-intercept (1, 0).

Go To Problems & Solutions Return To Top Of Page

10. The Common Logarithm

The logarithm of base 10, log₁₀ x, is called the common logarithm, and usually is denoted log x, without writing the base 10.
It's called so because it's commonly used in applications of mathematics. The exponential of base 10, 10^x, which is the inverse
of the common logarithm, is similarly called the common antilogarithm.

Consider the common logarithm y = log x. As shown in Fig. 10.1, when x increases for example from 1 to 1,000,000,
log x increases only from 0 to 6. So log x increases slowly. Also see the graph of log₁₀ x in Fig. 9.5. When x increases
from 1 to 10 thus by 10 – 1 = 9 units, log x increases from 0 to 1 hence by 1 – 0 = 1 unit; when x increases from 10 to
100 thus by 100 – 10 = 90 units, log x increases from 1 to 2 hence by 2 – 1 = 1 unit, still by 1 unit; when x increases from
100,000 to 1,000,000 thus by 1,000,000 – 100,000 = 900,000 units, log x increases from 5 to 6 hence by 6 – 5 = 1 unit, still by
1 unit. The larger x is, the slower log x increases. This can also be seen by examining the graph of log₁₀ x in Fig. 9.5 and the
derivative (rate of change) 1/(x ln 10) of log x. Clearly the larger x > 0 is, the smaller (down towards 0) 1/(x ln 10) becomes.
As x > 0 increases, log x increases slowly and at a decreasing rate. (The function y = (0.000,001)x increases slowly but at a
constant rate of dy/dx = 0.000,001; its graph is a straight line; that of y = log x is concave down).

Fig. 10.1 Common logarithm increases slowly and at a decreasing rate.

Return To Top Of Page

Problems & Solutions

1. Simplify the following expressions.

Solution

Return To Top Of Page

2. Solve the equation 5^2x3^2x–1 = 15^x–2 for x.

Solution

5^2x3^2x–1 = 15^x–2,

ln 5^2x3^2x–1 = ln 15^x–2,

ln 5^2x + ln 3^2x–1 = (x – 2) ln 15,

2x ln 5 + (2x – 1) ln 3 = x ln 15 – 2 ln 15,

x(2 ln 5 + 2 ln 3 – ln 15) = – 2 ln 15 + ln 3,

Return To Top Of Page

3. Differentiate the following functions.

a. f (x) = t^x – x^t.
b. g(t) = t^x – x^t.
c. y = log_a (bx + c).

Solution

a. f '(x) = t^x ln t – tx^t–1.

b. g'(t) = xt^x–1 – x^t ln x.

Return To Top Of Page

4. Consider the function y = (2x)^3x. The variable appears in both the base and the exponent. So the power rule and exponent
rule of differentiation don't apply to it directly.
a. Differentiate it by using the definition of the general exponential function.
b. Differentiate it by first taking the natural logarithm of both sides and then using implicit differentiation.
c. Are the answers in parts a and b the same?

Solution

a. y = (2x)^3x = e^{3x ln 2x},

y ' = e^{3x ln 2x} (3 ln 2x + 3x(2/2x)) = (2x)^3x (3 ln 2x + 3) = 3(2x)^3x (ln 2x + 1).

b. ln y = ln (2x)^3x = 3x ln 2x,
differentiate first and third sides implicitly:
y '/y = 3 ln 2x + 3x(2/2x) = 3 ln 2x + 3 = 3( ln 2x + 1),
y ' = y(3( ln 2x + 1)) = 3(2x)^3x (ln 2x + 1).

c. Yes.

Note

Of course in practice just use one method, unless you're asked to use both methods.

Return To Top Of Page

5. Prove that for any a > 0, any b > 0, and any c > 0, log_a b = log_a c log_c b.

Solution

log_a b = log_a c log_c b.

Return To Top Of Page Return To Contents