|
|
|
8.6
|
Return
To Contents
Go To Problems & Solutions
|
1. The Cauchy Mean-Value Theorem |
For a review of the mean-value theorem see Section 5.1 Theorem 5.1.

where D2, C2, G2, and F2 are the counterparts for point c of D, C, G, and F respectively.
|
|
Fig. 1.1
|
The property expressed by Eq. [1.1] is called the Cauchy
mean-value theorem or the generalized mean-value
theorem,
because from Eq. [1.1] we get:

Also note that Eq. [1.1] says that the ratio of the total
changes of f and g on [a, b]
is equal to the ratio of their
instantaneous rates of change at c.
Theorem 1.1 The Cauchy (Or Generalized) Mean-Value Theorem
|
|
Proof
Let:
h(x) = ( f(b) f(a))g(x) (g(b) g(a)) f(x).
Clearly h is continuous on [a, b] and differentiable on (a, b). Also:
h(a) = ( f(b) f(a))g(a) (g(b) g(a)) f(a) = f(b)g(a) f(a)g(b)
and:
h(b) = ( f(b) f(a))g(b) (g(b) g(a)) f(b) = f(b)g(a) f(a)g(b) = h(a).
So, by Rolle's theorem, there exists c in (a, b) such that h'(c) = 0. We have:
h'(x) = ( f(b) f(a))g'(x) (g(b) g(a)) f '(x),
yielding:
h'(c) = ( f(b) f(a))g'(c) (g(b) g(a)) f '(c).
Thus:
( f(b) f(a))g'(c) = (g(b) g(a)) f '(c).

EOP
The Cauchy mean-value theorem is also called the generalized mean-value theorem.
Go To Problems & Solutions Return To Top Of Page
|
|
In Section
1.1.3 we encountered limits of the indeterminate quotient form of type 0/0,
and in Section
1.1.7 we 
Remark that the right-hand side
is the quotient f '/g' of the derivatives f ' and g', not the derivative of the quotient f/g,
which is ( f 'g
fg' )/g2.
![]()
|
If:
|
Proof



The proofs for one-sided limits are contained in this proof.
The proofs for limits at infinity are similar to this proof.
EOP
![]()
Go To Problems & Solutions Return To Top Of Page
|
|
Example 3.1
Find:
![]()
Solution
![]()
EOS
Applying More Than Once
Example 3.2
Find:
![]()
Solution
![]()
EOS
![]()
Arranging Into Forms For The Rule
Example 3.3
Evaluate:
![]()
where a is a positive constant.
Solution
![]()
EOS
![]()
Trying To Simplify Before Trying To Apply The Rule
In Example 3.3, the limit:

So before trying to apply the rule we should first try to
simplify the limit's expression as much as possible. After
simplification it may or may not turn out that there's no more indeterminate
form. If you just keep applying the rule
without trying to simplify first, the process may never end.
For Functions Of The Form ( f (x)) g(x)
![]()
Example 3.4
![]()
Solution

EOS

When Not To Use The Rule
Trivially:

Go To Problems & Solutions Return To Top Of Page
|
|
|
|

For any given integer n > 0 we have:

EOP
Problems & Solutions |

Solution
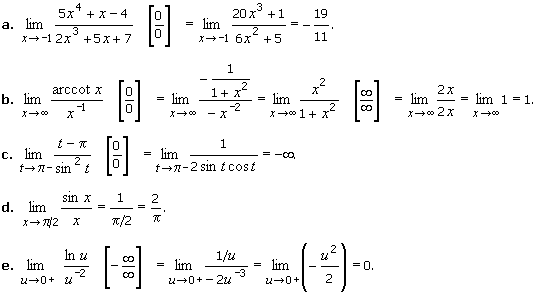
![]()
![]()
Solution

![]()

Solution

![]()
4. Consider this famous trigonometric limit:
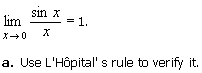
b. Can the computation in part a be considered
as another proof of that limit? Why or why not?
Solution

![]()
5. What's wrong with the following proof of the Cauchy mean-value theorem?
Since f
is continuous on [a, b] and differentiable
on (a, b), the mean-value
theorem implies that there exists c in
(a, b)
such that:

Solution
The proof assumes that there exists the same c that satisfies both equations [A] and [B], which is incorrect.
Return To Top Of Page Return To Contents



