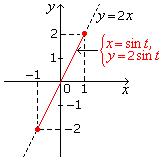Calculus Of One Real Variable – By Pheng Kim
Ving
|
|
|
Return To Contents
Go To Problems & Solutions
|
1. Parametric Curves |
In Section
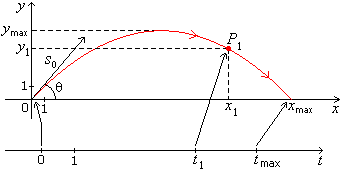
6.1.6 Part 2 we discussed the equations of the trajectory of the projectile
motion. The graph of the trajectory is
re-produced here in Fig. 1.1.
|
|
Fig.
1.1
Trajectory Of Projectile Motion.
The arrow head indicates the direction of motion.
|
First we found the set of 2 equations where t is the independent variable:
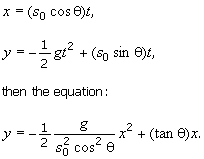
The 1st 2 equations are of the form x
= f(t), y = g(t), where f and g are continuous functions. We saw that these
equations
are called parametric equations, t is called
the parameter, and t is
non-negative. In Example
3.1 of the same section we
learned that t has a maximum value denoted by tmax. So the common domain of f
and g is I
= set of all real numbers between
0 and tmax inclusive. Here the parameter t is time. The last equation is of the form y = F(x). It's a Cartesian equation. It was
obtained from the parametric equations by eliminating t.
The graph of y = F(x) shown in Fig. 1.1 is the graph of the
corresponding parametric equations x = f(t), y = g(t). It's called a parametric curve.
The parametric curve is the path of the motion of the
object, because each point (x, y) on it is a position (x,
y) of the object in
the plane at time t, where x
= f(t) and y = g(t). The direction of the motion is
indicated by the arrow head. It of course
corresponds to increasing values of t. This
direction is also treated as the direction of the curve.
Fig. 1.2 is obtained by adding the t-axis
to Fig. 1.1 and changing a few labels. The t-axis is
different from the x-axis and y-axis.
At time t = 0 the object is at the origin; at
time t = t1 it's at
position P1 = (x1, y1), at time t = tmax it's at position xmax on the
|
|
Fig.
1.2
Position of object is function of time.
|
x-axis. Position of the object is a function of time.
In this section we take a closer look at parametric curves.
Definitions 1.1
– Parametric Curves
|
The set of equations: x = f(t), where f and g are continuous functions on a common domain
being some interval I of the
real line R
and t is an |
The parametric equations are an expressing of x and y in terms of
the parameter. Since f and g are functions, for each value
of t in the common domain of f and g there
corresponds exactly 1 value of x and exactly
1 value of y, thus exactly 1 point (x,
y) on the curve, where x
= f(t) and y = g(t).
A Function
Described By f And g
By the parametric equations x
= f(t), y = g(t), for each value of t
in the common domain I of f and g there
corresponds
exactly 1 point (x, y)
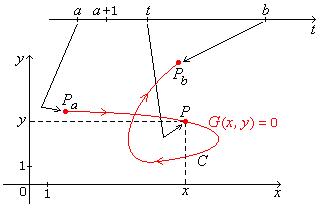
in the plane, where x = f(t) and y = g(t). See Fig. 1.3, where I
= [a, b]
with a < b.
Let C be the curve
formed by such points. We can view the equations as describing a function say h (not f or g, and not
a function or an equation
obtained by eliminating t) that maps
each real number t in I
to an ordered pair of real numbers (x, y) on C as follows:
h(t) =
(x, y)
= ( f(t), g(t)). It has
domain I on the real line and range C in the plane. It's a function from (a subset
of) R to (a subset
of) R2
(= R x R). Note that x
= f(t), y = g(t), and y = F(x) are
functions from R to R.
Curve Is Graph Of Cartesian Equation Or A
Part Of It
Suppose that from the parametric equations x = f(t), y = g(t) we get the
Cartesian equation y = F(x) or G(x, y) = 0 by
eliminating t. The parametric curve of the
parametric equations x = f(t), y = g(t) is the graph of the function y = F(x) or of
the equation G(x, y) = 0, because y
= F(x) or G(x, y) = 0 is derived from the parametric equations.
If there are restrictions
on x or y
by the nature of the parametric equations as will be shown in some examples
that follow, the curve may be just a
part of the graph of the Cartesian equation. It's called parametric
because of the parametric equations. Refer to Fig. 1.3. As for
the axes, the t-axis is different from the x-axis and the y-axis
of the xy-coordinate system of the plane of
the curve. Remark
that the curve in Fig. 1.3 is the graph of an xy-equation
G(x, y) = 0 that's not a function y
= F(x). We'll see
such curves in
some examples below.
If the Cartesian equation G(x, y) = 0 isn't
recognized or if 1 such equation isn't obtained from the parametric equations,
to
sketch the parametric curve in this section (another method is introduced in
the next section) we'll have to rely on the “lo-tech”
table of values to get a number of points, and we'll also use properties of the
curve if any, and then we'll join the points
together by a curve, as will be illustrated in an example below.
|
|
Fig. 1.3 Curve C of parametric
equations x = f(t), y = g(t) is graph
of |
Curve As Path Of Moving Object
Let P be the
point (x, y)
where x = f(t) and y = g(t), as in
Fig. 1.3. At t = a,
P is Pa.
As t increases, P
moves along the curve
C. At any t in [a, b], P is at a position (x,
y) on C. At t = b, P is at Pb.
The parametric equations x = f(t), y = g(t) specify
the coordinates (x, y)
of the point P at parameter value t, and P represents
an object moving in the plane. The parametric
curve C is the path of the moving object.
Since f and g
are continuous, C is continuous (has no breaks
in it).
Direction Of Curve
The direction of the curve C
is the direction of the motion of the object, and so it corresponds to
increasing values of t. To
determine the direction of the curve let's take an example. Suppose t is in [0, 5]. We calculate the positions (x, y) = ( f(t),
g(t)) at t = 0, 1, 2, 3, 4, and 5. From this we get the
direction of the motion of the object P(x, y) and thus
the direction of the
curve, which we indicate on the curve by arrow head(s). Clearly we have to rely
on the parametric equations to determine the
direction, which is lost in the Cartesian equation because it doesn't contain t.
Parameter
The parameter t is
sometimes referred to as time, because it often represents time. As
illustrated in the examples that follow,
it can represent other quantities, and letters other than t
can be used as parameter.
Return To Top Of Page Go To Problems & Solutions
Sketching By Eliminating The Parameter
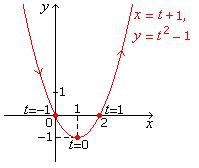
Example 2.1
a. Identify the parametric curve x
= t + 1, y
= t2 – 1, for all t
in R.
b. Sketch it.
c. Label the points corresponding to t = –1, t = 0, and t = 1.
d. Determine its direction and indicate the direction on it.
e. Give an example quantity that the parameter t
can represent.
Solution
a.
x = t
+ 1,
t = x
– 1,
y = t2 – 1 = (x
– 1)2 – 1 = x2 – 2x.
The curve is the parabola y
= x2 – 2x.
b.
y
= x2 – 2x
= x(x
– 2),
x-intercepts: x = 0 and 2,
y-intercept: y = 0,
y' = 2x
– 2 = 2(x – 1),
y' = 0 at x
= 1,
if x = 1 then y = –1,
vertex: (1, –1),
y'' = 2 > 0, concave up,
curve is sketched in Fig. 2.1.
|
|
Fig. 2.1 Parabola For Example 2.1. |
e.
The parameter t
can represent time.
EOS

{2.1}
Fig. 1.2.
{2.2}
Fig. 1.3.
Elimination Of The Parameter By Using Formulas Or Identities
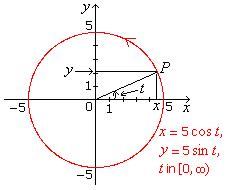
Example 2.2
![]()
Solution
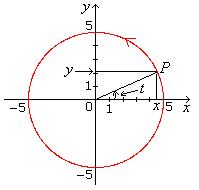
x2 + y2 = 25 cos2 t + 25 sin2 t = 25(cos2 t + sin2 t) = 25(1) = 52,
the curve is the circle with centre at the origin and radius 5, sketched in
Fig. 2.2.
|
|
Fig. 2.2 Circle For Example 2.2. |

An interpretation of t is that
it's the central angle associated with the point P(x, y).
EOS
Here the elimination of the parameter t
is easier by using a trigonometric identity, sin2 x + cos2 x = 1, than by direct
substitution for t as in Example 2.1. The
Cartesian equation x2 + y2 = 25 is recognized as that of a circle and isn't a
function.
The parameter t is interpreted as an angle,
since we're talking about its trigonometric functions. Remark that the circle
isn't
the unit circle; its radius is 5, not 1. For example, the perpendicular
projection x of P
on the horizontal axis is x = ((segment
joining 0 to P) times (cos t)) = 5 cos t,
not just cos t.
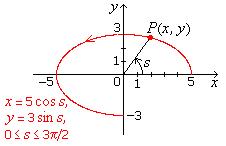
Restrictions On Parameter Specified With Parametric Equations
Example 2.3
![]()
Solution

|
|
Fig. 2.3 Partial Ellipse For Example 2.3. |
EOS
In Example 2.2 the coefficients of cos and
sin are equal, producing a circle. Here they're different,
producing an ellipse, or a
part of it due to restrictions on the parameter. The restrictions on the
parameter are specified with the parametric equations
and produce a partial ellipse.
Restrictions On x Or y Or Both That Aren't Contained In Cartesian Equation
Example 2.4
Sketch the curve having parametric representation x = sin t,
y = 2 sin t,
t in R. As t increases in R,
describe the motion of an
object whose position in the plane at time t is given by
these equations.
Solution

|
|
Fig. 2.4 “Curve” For Example 2.4. |
EOS
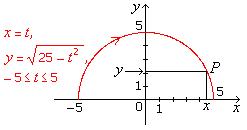
Example 2.5
![]()
Solution
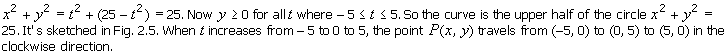
|
|
Fig. 2.5 Semi-Circle For Example 2.5. |
EOS
The restrictions that may be placed on x
or y by the nature of the parametric
equations may not be contained or apparent in
the Cartesian equation derived from them by eliminating the parameter. We must
examine this possibility carefully.

In Example 2.3, the restrictions are on the parameter and
are stated explicitly in the problem. The restrictions on x
and y also
exist, but they're also contained in the Cartesian equation. Remark that, for
that particular example, only a partial ellipse forms
the curve because of the restrictions on the parameter, not because of those on
x and y.
In Example 2.5, the direction of the curve is clockwise,
while in Example 2.2 it's counterclockwise. Clearly the direction of the
curve depends on the functions f and g.
Keep in mind that there are 2 kinds of restrictions: those
on the parameter, which are specified with the parametric equations,
and those on x and y,
which are implied by the nature of the parametric equations and aren’t
contained or apparent in the
Cartesian equation.
Sketching By Using Table Of Values And Properties Of Curve
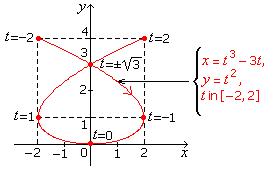
Example 2.6
Sketch the curve defined by the parametric equations x = t3 – 3t, y = t2, t in [–2, 2].
Use its properties if any. Indicate its
direction.
Solution
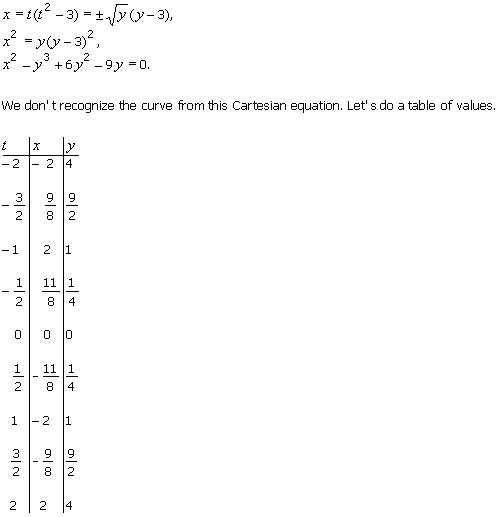
Symmetry. Now x is an odd
function of t and y
an even function of t. So at
opposite values of t, x has opposite values and y
has the same value. Thus the curve is symmetric about the y-axis.
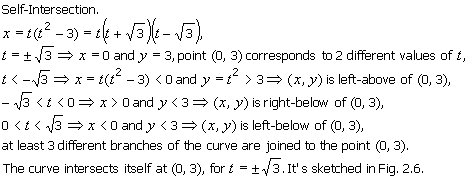
|
|
Fig. 2.6 Curve For Example 2.6. |
EOS
The curve isn't recognized from its Cartesian equation, so
we had to rely on the “lo-tech” table of values to get some points.
We also use the symmetry and self-intersection properties of the curve. A curve
self-intersects at a point if it passes thru that
point 2 or more times from different directions, ie there are 3 or more
different branches of it that are joined to that point,
which is passed thru for 2 or more different values of the parameter; so we look
for self-intersection at points (x, y) that each
correspond to 2 or more different values of the parameter. (A circle with
central-angle parameter in R passes thru every point
of it infinitely many times for different values of the parameter, but it doesn't
self-intersect, because the repeated passing is
done from the same single direction; there are only 2 branches of the circle
that are joined to each point.) Then we join the
points together by a curve. For clarity, points corresponding to fractional
values of t in the table of values aren't
labelled in
Fig. 2.6.
Return To Top Of Page Go To Problems & Solutions
|
3. Parametrization |
Above, from parametric equations we derive corresponding
Cartesian equations. Now we're going to perform the reverse.
From Cartesian equations we're going to derive corresponding parametric
equations. We're also going to determine parametric
equations of some curves whose equations, Cartesian or otherwise, aren't known
to us yet. To determine the parametric
equations of a curve is referred to as to parametrize it. The process of
determining parametric equations of a curve and the
parametric equations themselves are each referred to as parametrization
of the curve.
Since f and g in x = f(t) and y = g(t) are functions, where the parameter t is a particular quantity, for each value of t in the
common domain of f and g
there corresponds exactly 1 value of x and exactly
1 value of y, thus exactly 1 point (x, y) on the
curve, where x = f(t) and y = g(t). If this
rule is violated, then f or g or both don't exist, then the set of the 2
parametric
equations doesn't exist, then the curve can't be parametrized using the
particular quantity t as the
parameter.
Parametrization Of The Circle
In Example 2.2 we derive from the
parametric equations x = 5 cos
t, y = 5 sin
t the Cartesian equation x2 + y2 = 25. Now
suppose we're given the circle x2 + y2 = 25 and we're asked to parametrize it. To do this we
recall Example 2.2 and let x
=
5 cos t and y = 5 sin t,
then to verify we have x2 + y2 = 25 cos2 t + 25 sin2 t = 25(cos2 t + sin2 t) = 25(1) = 25. Or we let x
=
5 cos t and
calculate the t-expression for y. So a parametrization of the circle x2 + y2 = 25 is x = 5 cos t,
y = 5 sin t,
where t
is the central angle, as shown in Fig. 3.1.
|
|
Fig. 3.1 A parametrization of circle x2 + y2 = 25 is x = 5 cos t, y = 5 sin t,
where t is central |
Now let's see if there are other parametrizations of the circle x2 + y2 = 25. The following are its valid parametrizations:

The choice of a t-expression
for x must of course be such that x2 + y2 = 25 and the
selection for a t-interval must as a matter
of fact be such that x and y each assumes every value in [–5, 5] to get the
full circle. The cosine and sine functions can
produce infinitely many parametrizations of such a circle: x
= 5 cos h(t), y = 5 sin
h(t), or x = 5 sin h(t), y = 5 cos
h(t),
where h is a function of the form h(t) = tm or h(t) = mt and with a t-interval
such that x and y
have every value in [–5, 5]
(domain of h, which is the same as that of x and y because
cosine and sine are defined everywhere on R, is such
that the
ranges of x and y
both are [–5, 5]).
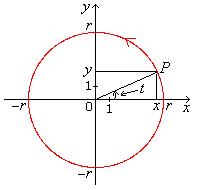
In general, there are infinitely many parametrizations of the circle x2 + y2 = r2. One of them where t is the central angle is:
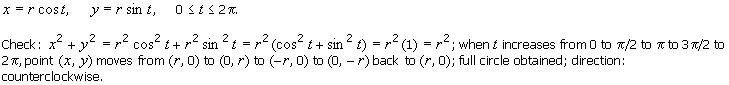
You should memorize it as it's often utilized:
|
A parametrization of the circle x2 + y2 = r2 using the central angle as parameter is:
start and finish point: (r,
0), |
|
|
Fig. 3.2 Parametrization of circle x2 + y2 = r2 using central angle is x = r cos t, y = r sin t. |
Parametrization Using A Specified Quantity As Parameter

(Notice the t-interval.
We must have the upper semi-circle only.) In this case the central angle is the
quantity specified to be
used as parameter.
Example 3.1
Parametrize the parabola y = x2 using its slope m at each point of it as parameter.
Solution
The slope of the parabola at each point (x, y) of it is m = y' = 2x. Then x = m/2 and y = x2 = (m/2)2 = m2/4. So the
desired
parametrization is x = m/2, y = m2/4, m in R.
EOS
We express both x and y in terms of the slope m.
For this purpose we determine an equation that relates x
to m. To obtain
the entire parabola, the m-interval
must be the entire set of real numbers, R. This
example is simple enough that we don't
have to draw a picture for help if not asked to.
In general, to use a specified quantity as parameter we have to determine an equation that relates x or y to that quantity.
Parametrization Using A Specified Quantity As Parameter Isn't Always Possible
Example 3.2
Can you parametrize the curve y
= x2 using as parameter the distance d from the general point (x,
y) on the curve to the
origin (0, 0)? Why or why not?
Solution
![]()
So no we can't, because each non-0 value of d corresponds to opposite values of x, thus to 2 different points (x, y) and (–x,
(–x)2) = (–x,
x2) = (–x, y) on the curve.
EOS
The right-most expression gives the same value of d from opposite values of x.
Each non-0 value of d corresponds
to 2
different values of x, so to 2
different points on the curve, violating the rule that each value of the
parameter corresponds to
exactly 1 point.
Example 3.3 – The Involute Of A Circle
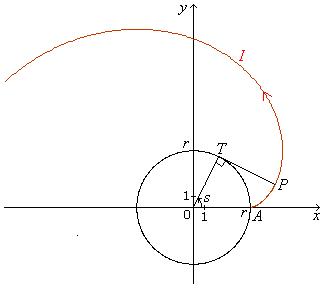
A string is wound around a circle with equation x2 + y2 = r2. See Fig. 3.3. One end at the point A
= (r, 0) is unwound in such a
way that the part of the string not lying on the circle is extended in a
straight line. The curve I followed by
this free end of the
string is called an involute of the circle. Let P
be the position of the free end of the string at some subsequent time and let T
be the point where the string leaves the circle. Clearly PT
is tangent to the circle at T. The path
of P is the involute. Let O be
the origin (0, 0). Parametrize the involute employing the central angle TOA, denoted by s,
as parameter.
|
|
Fig. 3.3 Curve I is involute of circle. |
Solution
|
|
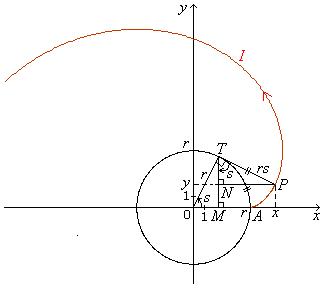
Fig. 3.4 Parametrization Of Involute Of Circle Employing Central
Angle As |
Refer to Fig. 3.4. Let (x, y) be the coordinates of P,
M the perpendicular projection of T on OA, and N the perpendicular
projection of P on TM.
Then:
x = OM + NP, y = MT – NT,
OM = OT cos
s = r cos
s,
angle NTP = angle MTP
= angle MOT = s,
as arms of angle MTP are perpendicular to those
of angle MOT,
PT = arc AT = rs, as s rad = (arc AT )/r,
NP = PT sin
s = rs sin
s,
x = r cos
s + rs sin
s;
MT = OT sin s
= r sin s,
NT = PT cos
s = rs cos s,
y = r sin
s – rs cos
s.
The required parametrization is:
![]()
EOS
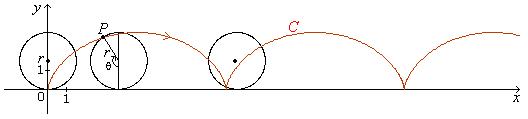
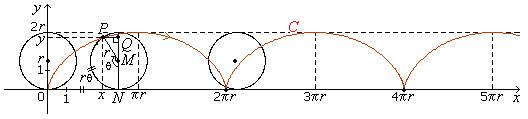
Example 3.4 – The Cycloid
When a circle rolls along a straight line, the path traced
by a point on it is called a cycloid. See Fig. 3.5. Suppose the circle
has
radius r, lies above the x-axis, rolls along the x-axis
starting from the origin O(0, 0) and
rolling to the right. Let P be a point
on
the circle and suppose it's originally at the origin.
![]()
2. Determine the x-intercepts,
the x-coordinates corresponding to the
maximum y-value, and the maximum y-value of the
cycloid by using:
a. Properties of the circle.
b. The parametric equations.
Indicate these values on the graph.
3. Show that (the horizontal component of the motion
of) any point P on the circle never moves
back as the circle rolls along
by using:
a. Geometry. Consider only
the lower semi-circle, as it's only there that points seem to move back.
b. Calculus.
|
|
Fig. 3.5 Curve C is cycloid. |
Solution
1.
|
|
Fig. 3.6 Parametrizing The Cycloid In |
Refer to Fig. 3.6. Take q
to be positive as the circle rolls along to the right. Let (x, y) be the
coordinates of P, M
the centre of
the circle, N the point where the circle touches
the x-axis, and Q
the perpendicular projection of P on MN. Then:
x = ON – PQ, y = NM + MQ = r + MQ,

|
|
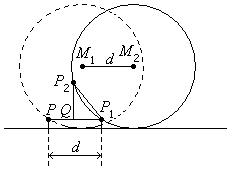
Fig. 3.7
As circle rolls along, any point on it never moves back. |
EOS
Contrary to what we may intuitively think, (the horizontal
component of the motion of) any point P on the
lower semi-circle
never moves back as the circle rolls along. An experiment to generate the
cycloid is easy and cheap to set up and carry out.
Physical Properties Of The Inverted Cycloid
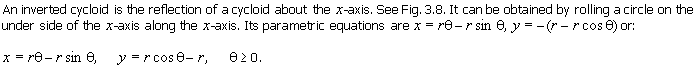
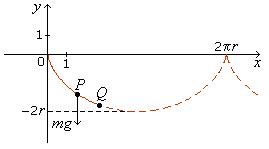
Brachistochrone Property
The word “brachistochrone” comes from 2 Greek words that
mean “shortest time”. Let Q be a given
point in the 4th quadrant.
Suppose a small object slides without friction from the origin O(0, 0) along a curve to Q
subject only to the downward force
mg due to gravity. What's the shape of the curve
that causes the object to slide from O to Q in the least or shortest possible
time? Initially we might think that it should be the straight line, as the
straight-line segment joining O and Q represents the
shortest distance between the 2 points. However the straight line isn't the
answer. It can be shown that the answer is a portion
|
|
Fig. 3.8 Physical Properties Of Inverted Cycloid. |
of an arc of an inverted cycloid generated by a point P on a circle of radius r
rolling on the under side of the x-axis along
the
x-axis, with P starting at
O, r being such
that the cycloid contains Q, and the
portion being between O and Q. This answer
appears to be reasonable: the curve should drop more steeply at first to allow
the object to gain speed more quickly.
Tautochrone Property
The word “tautochrone” comes from 2 Greek words that mean
“same time”. Let an object be placed at a point other than the
low point on an arc of an inverted cycloid. It can be shown that the time
required for it to slide to the low point is the same
for every initial point where it's placed. In other words, the time required
for it to slide to the low point is independent of the
initial point where it's placed.
Return To Top Of Page Go To Problems & Solutions
|
4. Plane Curves |
A plane curve is a continuous set of points in the plane
that can be described by an xy-Cartesian-equation
or a set of 2
parametric equations, as distinguished from plane regions. Clearly the parabola
y = x2 and the circle
x2 + y2 = 1 are plane
curves. They have Cartesian and parametric equations. Also clearly the involute
of a circle and the cycloid are plane curves.
They have parametric equations. So we use the parametric equations to define
plane curves. A plane curve is a curve that can
be described by a set of 2 parametric equations.
Definition 4.1 –
Plane Curves
|
A set of points
in the plane is said to be a plane curve if it's the parametric curve x = f(t), y = g(t), t in I, where f and g
|
Problems & Solutions |
1.
a. Sketch the parametric curve x = t2 , y = t3, for all t in R.
b. Label the points corresponding to t = –1, t = 0, and t = 1.
c. Determine the direction of the curve and indicate the direction on
it.
d. Give an example quantity that the parameter t
can represent.
Solution
a.
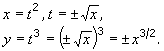
The curve is formed by the graphs of y = x3/2 and y = –x3/2.
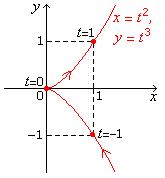
b.
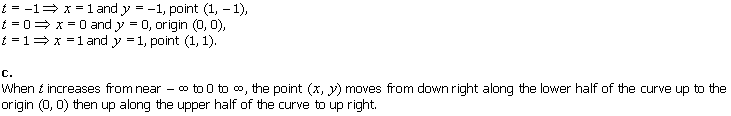
d.
The parameter t can represent time.
Note

Without examining the t-interval
which implies that y takes on
negative values as well as positive ones we may not realize that
obtaining only the upper half of the curve is incorrect. Thus it's a good idea
to always examine it and its implications.
![]()
![]()
Solution

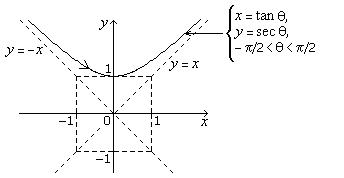
![]()
![]()
Solution

its direction is clockwise.
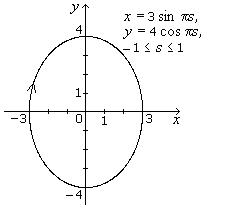
![]()
4. Sketch the curve having parametric representation x = t2,
y = t2 + 1, t
in R. As t increases
in R, describe the motion of an
object whose position in the plane
at time t is given by these equations.
Solutions
y = t2 + 1 = x + 1.
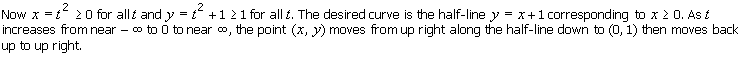
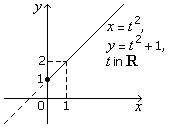
![]()
![]()
Solution

![]()
6. Can you parametrize the graph of y = x4 employing as
parameter the following quantities at the general point (x,
y) of the
graph? Why or why not?
a. The first derivative m.
b. The second derivative s.
c. The third derivative t.
d. The fourth derivative f.
Solution
a.
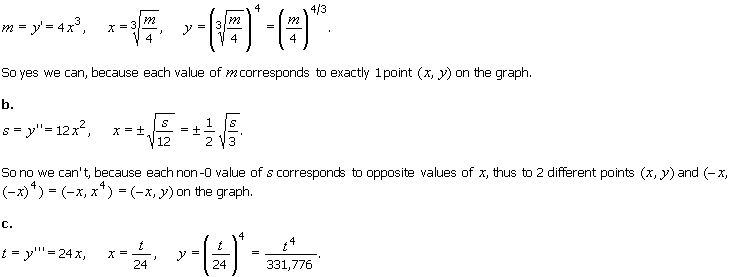
So yes we can, because each value of t corresponds to exactly 1 point (x, y) on the graph.
d.
f = y(4) = 24.
So no we can't, because the single value of f corresponds to (infinitely) many points (x, y) on the graph.
![]()


Solution
a.

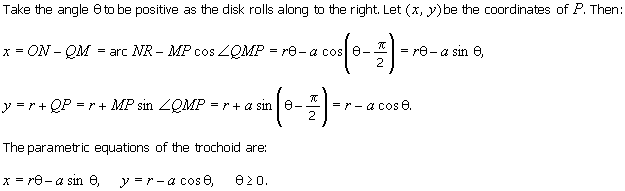
b.
If a = 0 then the curve is the horizontal line y = r.
c.
If a = r then the curve is a cycloid.
Return To Top Of Page Return To Contents