Return To Contents
Go To Problems & Solutions

In this section, we'll use the following abbreviations:

The name “Euler” is pronounced like the noun “oiler”. Leonhard Euler (1707–1783) was born in Switzerland, but spent most of his career in St Petersburg and Berlin. He was one of the leading mathematicians of the mid-18th century and one of the most prolific mathematicians of all time.

In this section we're going to discuss a method, called Euler method, to determine approximate numerical solutions of the initial-value problem (IVP) of the form y ' = f (x, y), y(x₀) = y₀. We must distinguish between y and f : y is the function such that y ' = f (x, y), f  is the given or known expression of y ', so y isn't f (x). For example, if y ' = x + y, then f (x, y) = x + y. The motivation for the development of the Euler method is the same as that for the development of the method of direction field, as seen in Section 16.4.1.

In Section 16.4.1, to assure ourselves that the direction field (DF) of a differential equation (DE) indeed generates approximate graphical solutions of the DE, we considered the DE y ' = x + y that can be solved exactly, solved it, drew some exact-solution curves, sketched the DF of the DE, and saw that the DF was consistent with the exact-solution curves and so indeed generated approximate graphical solutions of the DE. The general solution of this DE is y = Ce^x - x - 1, where C is an arbitrary constant.

Similarly, here we again use the DE y ' = x + y to assure ourselves that the approximate numerical solution by Euler method of a particular solution of this DE indeed approximates that particular solution. Since we deal with particular solutions, we'll work on IVPs.

Approximation Of Values Of Functions

But first we recall the approximation of values of functions. As shown in Section 8.3, we can approximate f (a + h) by f (a) + hf '(a) when we know the values of f (a), h, and f '(a). Because the letter f is used for the rate function y ' = f (x, y), let's utilize the letter g in place of f  for the function whose value at a + h is approximated by an expression involving its value at a. So we can approximate g(a + h) by g(a) + hg '(a) when we know the values of g(a), h, and g '(a), that is:

if h is sufficiently small (small = close to 0, not close to minus infinity). See Fig. 1.1. The oblique line in this picture is the tangent of the graph of y = g(x) at the point x = a. The value of the function at a + h is estimated by the value of the tangent line at that point. Approximation [1.1] is called the linear or tangent-line approximation.

Euler Method

We're considering the IVP of the general form:

where x₀ and y₀ are known or given constants. Look at Fig. 1.2. Since y₀ = y(x₀), we get the point (x₀, y₀), which is on the curve of the exact solution. We don’t know the exact value of y at any other point x. So at the next point x₁ a distance of h > 0 to the right of x₀ we use the linear approximation (LA) and the exact value (EV) y₀ = y(x₀) to approximate the EV y(x₁) by the approximate value (AV) y₁:

y₁ = y₀ + hy'(x₀, y₀) = y₀ + h f (x₀, y₀).

At the next point x₂ a distance of h to the right of x₁, we use the LA and the AV y₁, because we don’t have the

EV y(x₁), to approximate the EV y(x₂) by the AV y₂:

y₂ = y₁ + hy'(x₁, y₁) = y₁ + h f (x₁, y₁).

Similarly, at the next point x₃ a distance of h to the right of x₂, we use the LA and the AV y₂, because we don’t have the EV y(x₂), to approximate the EV y(x₃) by the AV y₃. And so on.

Note that y₁ isn't the EV of the solution y at x₁; it's an AP. The EV of course is denoted y(x₁). In general, y_n is the AV and y(x_n) is the EV of the solution y at x_n, n = 1, 2, . . .

A Particular Case

We illustrate the Euler method in a particular case, the case of the IVP:

Because the general solution of y' = x + y is y(x) = Ce^x - x - 1, we have:

2 = y(0) = Ce⁰ - 0 - 1 = C - 1,
C = 3.

So the exact solution of our IVP [1.2] is y = 3e^x - x - 1, whose graph is sketched in Fig. 1.3 together with the DF of the DE in the IVP [1.2]. In this section when we say “solution” without the qualifier “exact” or “approximate”,

it's understood to mean the exact solution.

In the calculations below, we pretend that we don't know that the exact solution of the IVP [1.3] is y = 3e^x - x - 1. Let f (x, y) = y ' = x + y. Because the value of the solution at x = 0 is given or known (here it's y = 2), we employ the point x₀ = 0 as the starting point from which we go to the right to do the approximation. See Fig. 1.3. We'll find the Euler approximate values of the solution at the points:

x₁ = x₀ + 0.5 = 0 + 0.5 = 0.5,
x₂ = x₁ + 0.5 = 0.5 + 0.5 = 1,
x₃ = x₂ + 0.5 = 1 + 0.5 = 1.5, and
x₄ = x₃ + 0.5 = 1.5 + 0.5 = 2.

These points are equally spaced by a horizontal distance of h = 0.5 x-unit. This distance is the size of the step that we make in travelling horizontally to the right, and consequently is called the step size  of the approximation.

Let y₀ be the exact value (EV) of the solution curve y = y(x) at x₀ = 0, so that y₀ = y(x₀) = y(0) = 2. Refer to Fig. 1.4. We plot the point (x₀, y₀) = (0, 2) in Fig. 1.4. By the LA we have:

y₁ = y₀ + hf (x₀, y₀) = 2 + (0.5) f (0, 2) = 2 + (0.5)(0 + 2) = 3,
y₂ = y₁ + hf (x₁, y₁) = 3 + (0.5) f (0.5, 3) = 3 + (0.5)(0.5 + 3) = 4.75,
y₃ = y₂ + hf (x₂, y₂) = 4.75 + (0.5) f (1, 4.75) = 4.75 + (0.5)(1 + 4.75) = 7.63,
y₄ = y₃ + hf (x₃, y₃) = 7.63 + (0.5) f (1.5, 7.63) = 7.63 + (0.5)(1.5 + 7.63) = 12.19.

We plot the points (x₁, y₁) = (0.5, 3), (x₂, y₂) = (1, 4.75), (x₃, y₃) = (1.5, 7.63), and (x₄, y₄) = (2, 12.19) in Fig. 1.4.

Note that in calculating y₁, of course we use the previous point (x₀, y₀), which is a point on the exact solution. But in calculating y₂, we don't know the previous point (x₁, y(x₁)) on the exact solution to use, otherwise we wouldn't

waste time determining the AV y₁ of y(x₁). So we use the point (x₁, y₁), and we utilize the lineal element of the DF that passes thru that point as an approximation of the solution curve near that point. Similarly for y₃ and y₄.

Remark that in the computations of y_i = y_i-1 + h f (x_i-1, y_i-1), which is the Euler AV of y(x_i) at x_i, the point x_i itself doesn't appear in the formula, which could mean that it wouldn't play a role in computing the AV of the function y at it, which in turn doesn't seem to be right. However it does play a role, by the presence of h, which is the distance from its previous point x_i-1 to it.

Now let's join consecutive points by line segments, as done in Fig. 1.5. By Fig. 1.5 we're now assured that the Euler method applied on the solution of an IVP indeed produces an approximation of that solution, at least for a number of small steps. The set of the values (0, 2), (0.5, 3), ..., (2, 12.19) is the Euler approximate numerical solution  of the IVP [1.2]. The polygon obtained by joining these points consecutively by line segments, colored blue in Fig. 1.5, is the graph of the Euler approximation.

Better Approximations

Let's reduce the step size from h = 0.5 to h = 0.25. As evidenced in Fig. 1.6, this smaller step size provides a better approximation than do larger ones. However reducing the step size increases the number of steps and

thus the number of points x where to calculate the approximations and consequently the number of calculations and hence the number of roundings. However, even though the number of roundings increases, generally a smaller step size still offers a better approximation than a larger one does.

The reason for the better approximation is as follows. In Fig. 1.6, the solid blue ellipse above x = 0.50 actually consists of 2 points. One point is on the curve for h = 0.50 and the other on that for h = 0.25. At x = 0.50, using h = 0.50 you make 1 action of approximation, at x = 0.50, while using h = 0.25 you make 2 actions, one at x = 0.25 and the other at x = 0.50 (if, eg, you use h = 0.1, then you make 5 actions, one at each of x = 0.10, 0.20, . . ., 0.50). At x = 1.00, using h = 0.50 you make 2 actions, while using h = 0.25 you make 4 actions (if, eg, you use h = 0.1, then you make 10 actions), etc. At any point x common to 2 or more step sizes, a smaller step size makes more actions of approximation than a larger one does, and therefore provides a better approximation at that point.

Return To Top Of Page     Go To Problems & Solutions

Observe that in Fig. 1.5 the slope of the exact solution curve at the initial point (x₀, y₀) = (0, 2) is of course also the slope of the lineal element of the direction field at that point.

In general, for the first-order IVP:

the aim of the Euler method is to determine AVs of the solution of this IVP at equally-spaced points:

x₁ = x₀ + h,     x₂ = x₁ + h, = x₀ + 2h,     . . .,     x_n = x_n-1 + h = x₀ + nh,

where h is the constant distance between consecutive points and is called the step size. According to the DE in [2.1], the slope of its DF at (x₀, y₀) is f (x₀, y₀). So, by the LA, the AV y₁ at x₁ is:

y₁ = y₀ + h f (x₀, y₀),

as shown in Fig. 2.1. Similarly, the slope of the DF at (x₁, y₁) is f (x₁, y₁), and the AV y₂ at x₂ is:

y₂ = y₁ + h f (x₁, y₁),

as shown in Fig. 2.2. In general, the AV y_n at x_n is:

y_n = y_n-1 + h f (x_n-1, y_n-1),

for n = 1, 2, . . .

Remark 2.1 – On Notations And Terminology

a. The notation y_n doesn't denote the EV of the solution at x_n, it denotes an AV. The EV of course is denoted by

    y(x_n), the functional notation, as we all are already familiar with. Of course the Euler method doesn't give the

    exact solution of an IVP. It produces approximations. However by reducing the step size we get successively

    better approximations of the exact solution.

b. Notice the distinction between the terminologies “method” and “approximation”: the Euler method is a method

    that produces approximations called, of course, the Euler approximations.

Example 2.1

Consider the IVP:

a. Use the Euler method with step size h = 0.2 and 10 steps to calculate the AVs y₁, y₂, . . ., y₁₀ of its solution.

    Round your answers to 2 decimal places. Construct a table to organize these approximations.

b. Plot these values and join the plotted points consecutively by line segments.

Solution

a. x₀ = 0, y₀ = 2, h = 0.2, f (x, y) = x + y,
    x_n = x_n-1 + h = x_n-1 + 0.2, n = 1, 2, . . ., 10,
    y_n = y_n-1 + hf (x_n-1, y_n-1) = y_n-1 + (0.2)(x_n-1 + y_n-1), n = 1, 2, . . ., 10,

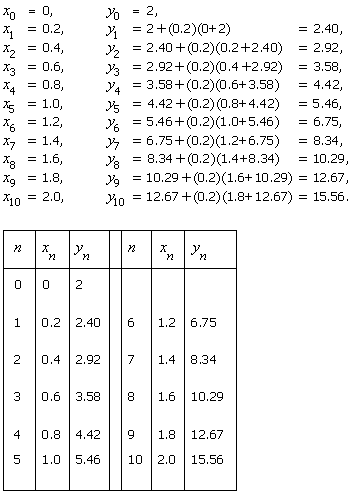
b. The plot is depicted in Fig. 2.3.

EOS

Remark 2.2 - On Example 2.1

A step size generates exactly 1 AV at any approximation point. We say that x is an approximation point if it’s a point where the approximation is performed. In Example 2.1, the approximation points are x₁ = 0.2, x₂ = 0.4, etc.

Using Computers

As seen earlier, for smaller and smaller step sizes, we get better and better approximations. In Example 2.1, given that the number of steps is 10, there are 10 values to calculate, and x₁₀ = 2. Suppose we consider the step size h = 0.1. If we wish to reach x = 2, there would be (2 - 0)/0.1 = 20 values to calculate, and 2 = x₂₀. In general, given an x-range on which to perform the approximation, of course for smaller and smaller step sizes, the approximation becomes better and better, but the amount of calculations becomes more and more considerable, so we should program a computer or use a computer program to carry out these calculations.

Example 2.2 – Using A Computer For Calculations

For the IVP of Example 2.1, which is y' = x + y, y(0) = 2, use a computer to compute the Euler estimates with 5 decimal places of y(1) and y(1.5) for the 10 step sizes h = 0.5, 0.25, 0.1, 0.05, 0.025, 0.01, 0.005, 0.0025, 0.001, and 0.0005, and construct a table of these estimates.

Notes

a. Each step size h is such that x = 1 and x = 1.5 are among the x_n's. For any step size h, y(1) and y(1.5) are

    estimated by y_m and y_k respectively for some positive integers m and k, where m < k and both depend on h.

b. Even though the question asks to find estimates of only y(1) and y(1.5), if we do the computations by hand then, for this example, for each step size we would still have to compute all the y_n's for n = 1, 2, . . ., m, where m is such that x_m = 1.5, because to calculate y_n we need to know y_n-1, for n = 1, 2, ..., m. For h = 0.0005, there are (1.5 - 0)/0.0005 = 3000 y-values to compute, each computation consists, as seen in the solution of Example 2.1, of 2 additions and 1 multiplication, for a total of 3 x 3,000 = 9,000 arithmetic operations. That's a lot! And that's for just 1 step size, although all other step sizes are larger and thus each require fewer computations. Computers therefore are absolutely welcome.

c. If we plot the points resulting from the approximations, then we expect something that looks similar to Fig.
   2.4, provided that all the AVs are less than the EVs.

Solution

EOS

Remarks 2.3 - On Example 2.2

a. A step size generates exactly 1 AV at x = 1 and exactly 1 AV at x = 1.5.

b. After constructing the table in Fig. 2.5, we realize that our plotted points in Fig. 2.4 are a little too high. But that's ok, since the set of those points is, as we said, similar to, not exactly like, the real thing.

c. In Fig. 2.5, the Euler estimates appear to approach limits, which must be the true values of y(1) and y(1.5) of the exact solution of the IVP respectively.

Example 2.3 – Using A Computer For Sketching

For the IVP of Example 2.1, which is y' = x + y, y(0) = 2, use a computer to sketch the graphs of the Euler approximations of the solution for the 5 step sizes h = 0.2, 0.1, 0.05, 0.02, and 0.001 for the interval [0, 2].

Solution

EOS

Remarks 2.4 - On Example 2.3

a.  Each step size h must be such that the last point x_n equals 2.

b. In Fig. 2.6, each x-interval represents 0.2 unit. So, for h = 0.2, each interval contains 1 step excluding its left endpoint, thus 1 point where to do the approximation; for h = 0.1, each interval contains 0.2/0.1 = 2 steps excluding its left endpoint, thus 2 points where to do the approximations; for h = 0.001, each interval contains 0.2/0.001 = 200 steps excluding its left endpoint, thus 200 points where to do the approximations. Each graph is actually a sequence of consecutively-joint line segments. As h gets smaller and smaller, the line segments in this example become shorter and shorter because their count in each interval of fixed length 0.2 unit gets larger and larger, hence the graphs look more and more like smooth curves.

c.  As h approaches 0, the graphs of the Euler approximations seem to approach a limit, which must be the graph of the exact solution of the IVP.

Determining A Formula For y_n And Determining The Number Of Steps

Example 2.4 - Formula For y_n And Number Of Steps

Consider the IVP:

Use the Euler method with step sizes h = 0.1, 0.01, 0.001, 0.0001, and 0.00001 to estimate y(2), without utilizing a computer. Do the AVs seem to approach a value? If yes, what value? Note: The exact solution is y = e^x. Hint: Find a formula for y_n in terms of y₀ (= y(0)), h, and n, and for each step size determine n such that y_n estimates y(2).

Note

For each step size, the x-points are x₀ = 0, x₁, x₂, . . ., x_n = 2, and n is such that y_n is the AV of y(2) for that step size. Remark that the subscript starts from 0, not 1, so there are n consecutive intervals: [x₀, x₁], [x₁, x₂], . . ., [x_n-1, x_n], and thus n steps and there would be n values to calculate. The length of each interval is the step size h. As a consequence, hn = x_n – x₀ = 2 – 0 = 2. Hence n = 2/h. If for each step size we calculate all the values y₁, y₂, . . ., y_n, there would be 2/0.1 + 2/0.01 + 2/0.001 + 2/0.0001 + 2/0.00001 = 222,220 values in total to calculate. And we're not allowed to utilize a computer. Because it's impractical to calculate all the 222,220 values by hand, especially in a test or exam, we have to determine a formula for y_n, which will be in terms of the known quantities y₀ and h and the readily-computed quantity n, as demonstrated in the solution. Then for each step size, we'll have to compute only 1 value, namely y_n.

Solution

We have x₀ = 0, y₀ = 1, and f (x, y) = y. So:

y_n = y_n-1 + h f (x_n-1, y_n-1)= y_n-1 + hy_n-1 = (1 + h)y_n-1 = (1 + h)(y_n-2 + hy_n-2) = (1 + h)(1 + h)y_n-2 = (1 + h)²y_n-2

    = (1  + h)²(y_n-3 + hy_n-3) = (1 + h)³y_n-3 = . . . = (1 + h)ⁿy_n-n = (1 + h)ⁿy₀. = (1 + h)ⁿ(1) = (1 + h)ⁿ.

For each step size h the number of steps is n = (2 - 0)/h = 2/h and y_n estimates y(2).

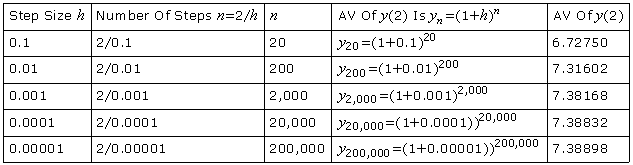
Yes, the AVs seem to approach a value, which must be the EV y(2) = e², which is approximately 7.38906.

EOS

Remark 2.5 - Number Of Step Sizes And Number Of Approximation Points

In Example 2.4, a step size generates exactly 1 AV at x = 2. Similar remarks are also made in Remarks 2.2 and 2.3. So to avoid confusion about the number of step sizes and the number of approximation points, we keep this in mind: a step size generates exactly 1 AV at any approximation point. For the definition of approximation point, see Remark 2.2.

Return To Top Of Page     Go To Problems & Solutions

We saw earlier under the heading Euler Method in this section that the exact solution of the IVP:

is y = 3e^x - x – 1. The Euler AVs of the solution for the step size h = 0.5 at the points x₁ = 0.5, x₂ = 1, x₃ = 1.5, and x₄ = 2 were calculated to be y₁ = 3, y₂ = 4.75, y₃ = 7.63, and y₄ = 12.19 respectively. Because the exact solution for this particular IVP is known, we can compare the AVs to the EVs. The error of the Euler method is of course the difference between the AV and the EV. The absolute error is the absolute value of the error. So:

error = AV - EV,
absolute error = |error| = |AV - EV|.

The AVs are estimates of the corresponding EVs. If an estimate is less than the EV, the error is negative, and we say that the estimate is an under-estimate (because it's under the EV). If an estimate is greater than the EV, the error is positive, and we say that the estimate is an over-estimate (because it's over the EV).

The table in Fig. 3.1 displays the EVs, the Euler AVs, the errors, and the absolute errors for the solution of [3.1] for the step size h = 0.5 at the indicated points x. As the exact solution itself involves the exponential function,

we have to settle with the decimal approximations of the EVs. Fig. 3.2 displays the exact-solution curve and the approximate-solution curve. Notice that as seen in Figs. 3.1 and 3.2, the absolute error increases as x moves to the right away from x₀, which is 0 in this case. Algebraically the error decreases, as a negative quantity that gets larger in size decreases, algebraically speaking. Saying that the error decreases would be misleading in its everyday sense. So to avoid this problem we employ the absolute error.

Fig. 1.6 is re-produced as Fig. 3.3. Clearly as the step size is halved from h = 0.5 to h = 0.25, the absolute error (here at the points x = 0.50, 1.00, 1.50, and 2.00) is roughly halved too.

In general, the absolute error in the Euler method possesses these properties:

1. For any 1 step size h, when x increases away from x₀, the absolute error tends to increase as well.

2.       At any 1 point x, when h decreases, the absolute error tends to be proportional to h. For example, decreasing

   h by half decreases the absolute error by approximately half as well.

These properties are studied in depth in courses on differential equations and courses on numerical analysis (numerical analysis is now sometimes also called scientific computations).

Return To Top Of Page     Go To Problems & Solutions

Suppose that we're given a DF, as displayed in Fig. 4.1, and that we're asked to sketch the graph of the Euler approximation of the exact solution curve that passes thru the point (0, 2), with step size 0.5 and 4 steps. This

is an IVP, with y(0) = 2, but we have only a DF instead of an explicit DE of the form y ' = f (x, y). So of course we cannot use the formula y_n = y_n-1 + h f (x_n-1, y_n-1). We have to utilize the DF itself.

Recall that the formula y_n = y_n-1 + hf (x_n-1, y_n-1) is the tangent-line approximation, as seen in Fig. 1.2 for n = 1, re-produced below for convenience as Fig. 4.2. We draw the tangent line of the curve at the point (x_n-1, y_n-1), this tangent intersects the vertical line x = x_n at a point, the y-coordinate of this point is y_n, this point is the desired point (x_n, y_n). Let's employ a similar process for a DF. Refer to Fig. 4.3, which is Fig. 2.2 re-produced here for

convenience. For example, at the point (x₁, y₁), we draw a tangent line from that point that's parallel to the lineal element at that point, or parallel to the lineal element nearest to that point. That tangent intersects the vertical line x = x₂ at the point (x₂, y₂).

Now let's draw the graph of the Euler approximation. See Fig. 4.4. First we draw dashed vertical lines at x = 0.5, 1.0, 1.5, and 2.0. Then from the point (0, 2) we sketch a line segment parallel to the lineal element nearest to that point till it intersects the line x = 0.5. Next from that point of intersection we sketch a line segment parallel to the lineal element nearest to that point till it intersects the line x = 1.0. We repeat the process for all the remaining steps. The required graph of the Euler approximation is the sequence of these line segments.

Return To Top Of Page     Go To Problems & Solutions

The idea behind the numerical method for first-order ordinary differential equations is to approximate the numerical y-values of a solution for a given or chosen finite discrete sequence of x-values: x₁, x₂, . . ., x_n, equally spaced. We start at an initial point (x₀, y₀) on a solution curve and then calculate the y-values y₁, y₂, . . ., y_n that approximate the actual y-values y(x₁), y(x₂), . . ., y(x_n) respectively. The points (x₁, y₁), (x₂, y₂), . . . , (x_n, y_n) represent the approximations of the actual points (x₁, y(x₁)), (x₂, y(x₂)), . . . , (x_n, y(x_n)) respectively. The actual points are the ones that actually lie on the graph of the solution y(x), which is usually unknown. The value y₀ is the actual value of the solution at x₀. So what we do is to determine numerically an approximation of the solution that passes thru the point (x₀, y₀). Graphically, by joining the consecutive points (x₀, y₀), (x₁, y₁), . . . , (x_n, y_n) by line segments, we obtain a polygon, which hopefully has qualitative characteristics that are close to those of an actual solution curve.

The Euler method is simply one of many different numerical methods in which a solution of a DE can be approximated. Other numerical methods, notably the fourth order Runge-Kutta method, provide significantly greater accuracy than the Euler method does. However the Euler method is the place to start the learning of numerical methods for DEs.

Return To Top Of Page

1. Consider the IVP:

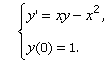
a. Use the Euler method with step size h = 0.25 and 10 steps to calculate the AVs y₁, y₂, . . ., y₁₀ of its solution. 

    Round your answers to 2 decimal places. Construct a table to organize these approximations.

b. Plot these values and join the plotted points consecutively by line segments.

Solution

a. x₀ = 0, y₀ = 1, h = 0.25, f (x, y) = xy - x²,
    x_n = x_n-1 + h = x_n-1 + 0.25, n = 1, 2, . . ., 5,

Return To Top Of Page

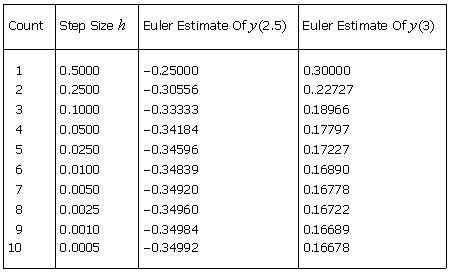
2. Use a computer to compute the Euler estimates with 5 decimal places of y(2.5) and y(3) for the 10 step sizes

    h = 0.5, 0.25, 0.1, 0.05, 0.025, 0.01, 0.005, 0.0025, 0.001, and 0.0005, and construct a table of these

    estimates, for this IVP:

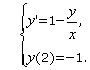
Solution

Return To Top Of Page

3. Consider the IVP:

   Solution

Return To Top Of Page

4. Consider the IVP:

a. Verify that its exact solution is y = (1.8)e^2x.

b. Use the Euler method with each of the following step sizes to estimate the value of y(1.5) without utilizing a
    computer: h = 0.1, 0.05, 0.025, 0.0125, 0.00625, and 0.003125. Note that each step size from the second on

    is half of the previous one. Do the AVs appear to tend to a value? If yes, what value?  Hint: Find a formula

    for y_n in terms of y₀ = 1.8, h, and n. For each step size, determine n such that y_n is the AV of y(1.5).
c. State which estimates are over-estimates and which are under-estimates.

d. Find the error and the absolute error in the Euler method in part b for each step size. Each time the step size
    is cut in half, what happens to the absolute error?

Solution

a. If y = (1.8)e^2x then y ' = 2(1.8)e^2x = 2y and y(0) = (1.8)e⁰ = 1.8. So y = (1.8)e^2x indeed is the exact solution of

    the given IVP.

b. We have x₀ = 0, y₀ = 1.8, and f (x, y) = 2y. So:

    y_n = y_n-1 + h f (x_n-1, y_n-1) = y_n-1 + h(2y_n-1) = (1 + 2h)y_n-1 = (1 + 2h)(y_n-2 + h(2y_n-2)) = (1 + 2h)²y_n-2
       =(1 + 2h)²(y_n-3 + h(2y_n-3)) = (1 + 2h)³y_n-3 = . . . = (1 + 2h)ⁿy_n-n = (1 + 2h)ⁿy₀ = (1.8)(1 + 2h)ⁿ.

    For each step size h the number of steps is (1.5 - 0)/h = 1.5/h.

    Yes, the AVs appear to tend to a value, which must be the EV y(1.5) = (1.8)e^2(1.5) = (1.8)e³, which is

    approximately 36.15397.

c. Because the EV is approximately 36.15397, all the estimates are under-estimates. There's no
    over-estimate.

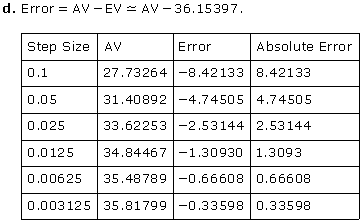
    Each time the step size is cut in half, the absolute error is roughly cut in half too.

Return To Top Of Page

5. For the IVP:

    show that, when using the Euler method with step size h, the estimate y_n of y(x_n) is given by the formula:

    y_n = (nh)² + (2 - h)nh + 2.

    Note that x_n-1 and y_n-1 don't appear in this formula.

Solution

We have x₀ = 1, y₀ = 2, and f (x, y) = 2x. So:

Note

We use the formula:

Return To Top Of Page

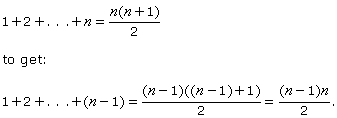
6. A DF for a DE is displayed below. Sketch the graphs of 2 Euler approximations of the solution curve that

    passes thru the point (0, 1). Use step sizes h = 0.5 and h = 0.25 and go till x = 2.

Solution

Return To Top Of Page

7. It can be shown that for the IVP y' = f (x, y), y(x₀) = y₀, as the step size h decreases toward 0, then the

    Euler approximations converge to the exact solution, provided f satisfies some conditions. This problem gives

    an example to illustrate this property of the convergence of the Euler method. Consider this IVP:

Solution

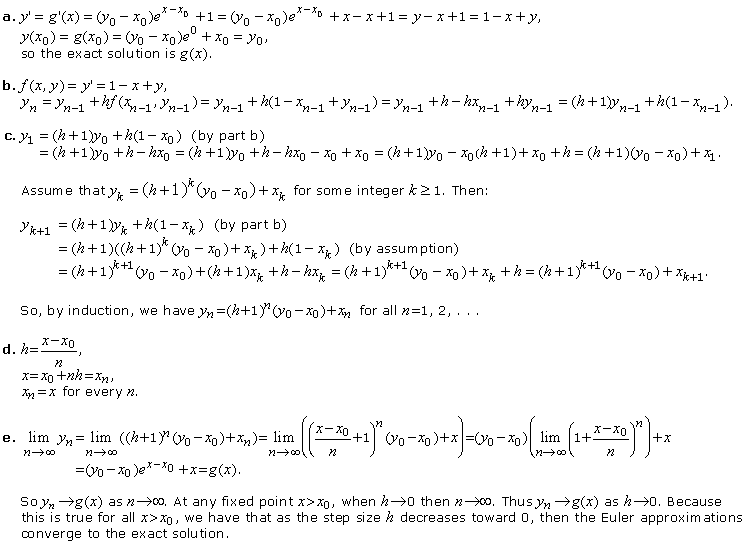
Return To Top Of Page     Return To Contents